��Ŀ����
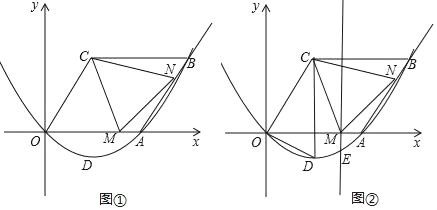
����Ŀ����ͼ������y=ax2+bx������A��4��0���͵�B��6��2![]() �����ı���OCBA��ƽ���ı��Σ���M��t��0��Ϊx���������ϵĵ㣬��NΪ����AB�ϵĵ㣬��AN=OM����DΪ�����ߵĶ��㣮
�����ı���OCBA��ƽ���ı��Σ���M��t��0��Ϊx���������ϵĵ㣬��NΪ����AB�ϵĵ㣬��AN=OM����DΪ�����ߵĶ��㣮
��1���������ߵĽ���ʽ����ֱ��д����D�����ꣻ
��2������AMN���ܳ���Сʱ����t��ֵ��
��3����ͼ�ڣ�����M��ME��x�ᣬ��������y=ax2+bx�ڵ�E������EM��AE������AME���DOC����ʱ����ֱ��д�����з��������ĵ�M���꣮
���𰸡���1��y=![]() x2��
x2��![]() x����D��������2����
x����D��������2����![]() ������2��t=2����3��M���������2��0����6��0����
������2��t=2����3��M���������2��0����6��0����
��������
��1�����ô���ϵ�����������߽���ʽ�������䷽����һ��ʽ��Ϊ����ʽ�õ���D�����ꣻ
��2������AC����ͼ�٣��ȼ����AB=4�����ж�ƽ���ı���OCBAΪ���Σ���֤����AOC����ACB���ǵȱ������Σ�����֤����OCM�ա�ACN�õ�CM=CN����OCM=��ACN�����ж���CMNΪ�ȱ������εõ�MN=CM��������AMN���ܳ�=OA+CM������CM��OAʱ��CM��ֵ��С����AMN���ܳ���С���Ӷ��õ�t��ֵ��
��3�������ù��ɶ������涨��֤����OCDΪֱ�������Σ���COD=90������M��t��0������E��t��![]() t2-
t2-![]() t�����������������ε��ж���������
t�����������������ε��ж���������![]() ʱ����AME�ס�COD����|t-4|��4=|
ʱ����AME�ס�COD����|t-4|��4=|![]() t2-
t2-![]() t |��
t |��![]() ����
����![]() ʱ����AME�ס�DOC����|t-4|��
ʱ����AME�ס�DOC����|t-4|��![]() =|
=|![]() t2-
t2-![]() t |��4��Ȼ��ֱ�����ֵ���̿ɵõ���Ӧ��M������꣮
t |��4��Ȼ��ֱ�����ֵ���̿ɵõ���Ӧ��M������꣮
��1����A��4��0����B��6��2![]() ������y=ax2+bx��
������y=ax2+bx��
![]() �����
�����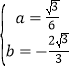 ��
��
�������߽���ʽΪy=![]() x2-
x2-![]() x��
x��
��y=![]() x2-
x2-![]() x =
x =![]() -2) 2-
-2) 2-![]() ��
��
���D��������2��-![]() ����
����
��2������AC����ͼ�٣�

AB=![]() =4��
=4��
��OA=4��
��ƽ���ı���OCBAΪ���Σ�
��OC=BC=4��
��C��2��2![]() ����
����
��AC=![]() =4��
=4��
��OC=OA=AC=AB=BC��
���AOC�͡�ACB���ǵȱ������Σ�
���AOC=��COB=��OCA=60����
��OC=AC��OM=AN��
���OCM�ա�ACN��
��CM=CN����OCM=��ACN��
�ߡ�OCM+��ACM=60����
���ACN+��ACM=60����
���CMNΪ�ȱ������Σ�
��MN=CM��
���AMN���ܳ�=AM+AN+MN=OM+AM+MN=OA+CM=4+CM��
��CM��OAʱ��CM��ֵ��С����AMN���ܳ���С����ʱOM=2��
��t=2��
��3����C��2��2![]() ����D��2��-
����D��2��-![]() ����
����
��CD=![]() ��
��
��OD=![]() ��OC=4��
��OC=4��
��OD2+OC2=CD2��
���OCDΪֱ�������Σ���COD=90����
��M��t��0������E��t��![]() t2-
t2-![]() t����
t����
�ߡ�AME=��COD��
�൱![]() ʱ����AME�ס�COD����|t-4|��4=|
ʱ����AME�ס�COD����|t-4|��4=|![]() t2-
t2-![]() t |��
t |��![]() ��
��
������|![]() t2-
t2-![]() t|=
t|=![]() |t-4|��
|t-4|��
�ⷽ��![]() t2-
t2-![]() t =
t =![]() ��t-4����t1=4����ȥ����t2=2����ʱM������Ϊ��2��0����
��t-4����t1=4����ȥ����t2=2����ʱM������Ϊ��2��0����
�ⷽ��![]() t2-
t2-![]() t =-
t =-![]() ��t-4����t1=4����ȥ����t2=-2����ȥ����
��t-4����t1=4����ȥ����t2=-2����ȥ����
��![]() ʱ����AME�ס�DOC����|t-4|��
ʱ����AME�ס�DOC����|t-4|��![]() =|
=|![]() t2-
t2-![]() t |��4��������|
t |��4��������|![]() t2-
t2-![]() t |=|t-4|��
t |=|t-4|��
�ⷽ��![]() t2-
t2-![]() t =t-4��t1=4����ȥ����t2=6����ʱM������Ϊ��6��0����
t =t-4��t1=4����ȥ����t2=6����ʱM������Ϊ��6��0����
�ⷽ��![]() t2-
t2-![]() t =-��t-4����t1=4����ȥ����t2=-6����ȥ����
t =-��t-4����t1=4����ȥ����t2=-6����ȥ����
����������M���������2��0����6��0����

 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�����Ŀ����һ�������ĺ�����װ��ֻ����ɫ��ͬ�ĺڡ���������40����С�����������飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣��±��������е�һ��ͳ�����ݣ�
����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ���m | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
���������Ƶ�� | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 | �� �� | �� �� |
��1������ϱ���
��2�����Ӻ������������һ��������������ĸ���P���� �������������С�����һλ��
��3��������������ĺ���������ж��ٸ���