题目内容
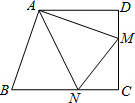如图，直角梯形ABCD中，AD∥BC，∠C=90°，点M在CD边上，AB=AM，AN平分∠BAM交BC于点N，连接MN．若BC=8，CM=4，则MN的长为5
5
．分析：由AB=AM，AN平分∠BAM交BC于点N，易证得△BAN≌△MAN，则可得MN=BN，然后设MN=x，即可得CN=8-x，然后由勾股定理即可求得方程：x2=（8-x）2+42，解此方程即可求得MN的长．
解答：解：∵AN平分∠BAM交BC于点N，
∴∠BAN=∠MAN，
在△BAN和△MAN中，
∵
，
∴△BAN≌△MAN（SAS），
∴BN=MN，
设MN=x，
则BN=x，CN=BC-BN=8-x，
∵∠C=90°，
在Rt△CMN中，MN2=CN2+CM2，
即x2=（8-x）2+42，
解得：x=5，
即MN=5．
故答案为：5．
∴∠BAN=∠MAN，
在△BAN和△MAN中，
∵
|
∴△BAN≌△MAN（SAS），
∴BN=MN，
设MN=x，
则BN=x，CN=BC-BN=8-x，
∵∠C=90°，
在Rt△CMN中，MN2=CN2+CM2，
即x2=（8-x）2+42，
解得：x=5，
即MN=5．
故答案为：5．
点评：此题考查了直角梯形的性质、全等三角形的判定与性质以及勾股定理．此题难度适中，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
相关题目
如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．
ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．
如图，直角梯形ABCD中，AD∥BC，∠BCD=90°，且CD=2AD，tan∠ABC=2．
（2013•深圳二模）如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60°．以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．
已知：如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，以AB为直径的⊙O切DC边于E点，AD=3cm，BC=5cm．求⊙O的面积．