ћвƒњƒЏ»Ё
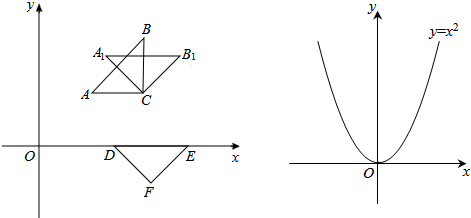
£®2013•“еќЏ –£©–°√чЇѕ„ч—Іѕ∞–°„й‘ЏћљЊњ–э„™°Ґ∆љ“∆±дїї£Ѓ»зЌЉ°чABC£ђDEFЊщќ™µ»—ь÷±љ«»эљ«–ќ£ђЄчґ•µг„ш±кЈ÷±рќ™A£®1£ђ1£©£ђB£®2£ђ2£©£ђC£®2£ђ1£©£ђD£®
£ђ0£©£ђE£®2
£ђ0£©£ђF£®
£ђ-
£©£Ѓ
£®1£©Ћы√«љЂ°чABC»∆Cµг∞іЋ≥ ±’лЈљѕт–э„™45°гµ√µљ°чA1B1C1£Ѓ«лƒг–і≥цµгA1£ђB1µƒ„ш±к£ђ≤Ґ≈–ґѕA1CЇЌDFµƒќї÷√єЎѕµ£ї
£®2£©Ћы√«љЂ°чABC»∆‘≠µг∞іЋ≥ ±’лЈљѕт–э„™45°г£ђЈҐѕ÷–э„™Їуµƒ»эљ«–ќ«°Ї√”–ЅљЄцґ•µг¬д‘Џ≈„ќпѕяy=2
x2+bx+c…ѕ£ђ«лƒг«у≥цЈыЇѕћхЉюµƒ≈„ќпѕяљвќц љ£ї
£®3£©Ћы√«Љћ–шћљЊњ£ђЈҐѕ÷љЂ°чABC»∆ƒ≥Єцµг–э„™45°г£ђ»ф–э„™Їуµƒ»эљ«–ќ«°Ї√”–ЅљЄцґ•µг¬д‘Џ≈„ќпѕяy=x2…ѕ£ђ‘тњ…«у≥ц–э„™Їу»эљ«–ќµƒ÷±љ«ґ•µгPµƒ„ш±к£ђ«лƒг÷±љ”–і≥цµгPµƒЋщ”–„ш±к£Ѓ
| 2 |
| 2 |
3
| ||
| 2 |
| ||
| 2 |
£®1£©Ћы√«љЂ°чABC»∆Cµг∞іЋ≥ ±’лЈљѕт–э„™45°гµ√µљ°чA1B1C1£Ѓ«лƒг–і≥цµгA1£ђB1µƒ„ш±к£ђ≤Ґ≈–ґѕA1CЇЌDFµƒќї÷√єЎѕµ£ї
£®2£©Ћы√«љЂ°чABC»∆‘≠µг∞іЋ≥ ±’лЈљѕт–э„™45°г£ђЈҐѕ÷–э„™Їуµƒ»эљ«–ќ«°Ї√”–ЅљЄцґ•µг¬д‘Џ≈„ќпѕяy=2
| 2 |
£®3£©Ћы√«Љћ–шћљЊњ£ђЈҐѕ÷љЂ°чABC»∆ƒ≥Єцµг–э„™45°г£ђ»ф–э„™Їуµƒ»эљ«–ќ«°Ї√”–ЅљЄцґ•µг¬д‘Џ≈„ќпѕяy=x2…ѕ£ђ‘тњ…«у≥ц–э„™Їу»эљ«–ќµƒ÷±љ«ґ•µгPµƒ„ш±к£ђ«лƒг÷±љ”–і≥цµгPµƒЋщ”–„ш±к£Ѓ

Ј÷ќц£Ї£®1£©”…–э„™–‘÷ Љ∞µ»—ь÷±љ«»эљ«–ќ±яљ«єЎѕµ«уљв£ї
£®2£© „ѕ»√ч»Ј°чABC»∆‘≠µг∞іЋ≥ ±’лЈљѕт–э„™45°гЇуµƒ»эљ«–ќЉіќ™°чDEF£ђ»їЇуЈ÷»э÷÷«йњцљш––ћ÷¬џ£ђЈ÷±рЉ∆Ћг«уљв£ї
£®3£©–э„™Јљѕт”–Ћ≥ ±’л°Ґƒж ±’лЅљ÷÷њ…ƒ№£ђ¬д‘Џ≈„ќпѕя…ѕµƒµг”–µгAЇЌµгB°ҐµгBЇЌµгC°ҐµгCЇЌµгD»э÷÷њ…ƒ№£ђ“тіЋє≤”–Ѕщ÷÷њ…ƒ№µƒ«й–ќ£ђ–и“™Ј÷јаћ÷¬џ£ђ±№√⬩љв£Ѓ
£®2£© „ѕ»√ч»Ј°чABC»∆‘≠µг∞іЋ≥ ±’лЈљѕт–э„™45°гЇуµƒ»эљ«–ќЉіќ™°чDEF£ђ»їЇуЈ÷»э÷÷«йњцљш––ћ÷¬џ£ђЈ÷±рЉ∆Ћг«уљв£ї
£®3£©–э„™Јљѕт”–Ћ≥ ±’л°Ґƒж ±’лЅљ÷÷њ…ƒ№£ђ¬д‘Џ≈„ќпѕя…ѕµƒµг”–µгAЇЌµгB°ҐµгBЇЌµгC°ҐµгCЇЌµгD»э÷÷њ…ƒ№£ђ“тіЋє≤”–Ѕщ÷÷њ…ƒ№µƒ«й–ќ£ђ–и“™Ј÷јаћ÷¬џ£ђ±№√⬩љв£Ѓ
љвір£Їљв£Ї£®1£©A1£®2-
£ђ1+
£©£ђB1£®2+
£ђ1+
£©£Ѓ
A1CЇЌDFµƒќї÷√єЎѕµ «∆љ––£Ѓ
£®2£©°я°чABC»∆‘≠µг∞іЋ≥ ±’лЈљѕт–э„™45°гЇуµƒ»эљ«–ќЉіќ™°чDEF£ђ
°аҐўµ±≈„ќпѕяЊ≠єэµгD°ҐE ±£ђЄщЊЁћв“вњ…µ√£Ї
£ђ
љвµ√
°аy=2
x2-12x+8
£ї
ҐЏµ±≈„ќпѕяЊ≠єэµгD°ҐF ±£ђЄщЊЁћв“вњ…µ√£Ї
£ђ
љвµ√
°аy=2
x2-11x+7
£ї
Ґџµ±≈„ќпѕяЊ≠єэµгE°ҐF ±£ђЄщЊЁћв“вњ…µ√£Ї
£ђ
љвµ√
°аy=2
x2-13x+10
£Ѓ
£®3£©‘Џ–э„™єэ≥ћ÷–£ђњ…ƒ№”–“‘ѕ¬«й–ќ£Ї

ҐўЋ≥ ±’л–э„™45°г£ђµгA°ҐB¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ1Ћщ Њ£Ї
“„«уµ√µгP„ш±кќ™£®0£ђ
£©£ї
ҐЏЋ≥ ±’л–э„™45°г£ђµгB°ҐC¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ2Ћщ Њ£Ї
…иµгB°д£ђC°дµƒЇб„ш±кЈ÷±рќ™x1£ђx2£Ѓ
“„÷™іЋ ±B°дC°д”л“ї°Ґ»эѕуѕёљ«∆љЈ÷ѕя∆љ––£ђ°а…и÷±ѕяB°дC°дµƒљвќц љќ™y=x+b£ђ
Ѕ™ЅҐy=x2”лy=x+bµ√£Їx2=x+b£ђЉіx2-x-b=0£ђ
°аx1+x2=1£ђx1x2=-b£Ѓ
°яB°дC°д=1£ђ°аЄщЊЁћв“в“„µ√£Ї|x1-x2|=
£ђ
°а£®x1-x2£©2=
£ђЉі£®x1+x2£©2-4x1x2=
°а1+4b=
£ђљвµ√b=-
£Ѓ
°аx2-x+
=0£ђљвµ√x=
їтx=
£Ѓ
°яµгC°дµƒЇб„ш±кљѕ–°£ђ°аx=
£Ѓ
µ±x=
±£ђy=x2=
£ђ
°аP£®
£ђ
£©£ї
ҐџЋ≥ ±’л–э„™45°г£ђµгC°ҐA¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ3Ћщ Њ£Ї
…иµгC°д£ђA°дµƒЇб„ш±кЈ÷±рќ™x1£ђx2£Ѓ
“„÷™іЋ ±C°дA°д”лґю°ҐЋƒѕуѕёљ«∆љЈ÷ѕя∆љ––£ђ°а…и÷±ѕяC°дA°дµƒљвќц љќ™y=-x+b£ђ
Ѕ™ЅҐy=x2”лy=-x+bµ√£Їx2=-x+b£ђЉіx2+x-b=0£ђ
°аx1+x2=-1£ђx1x2=-b£Ѓ
°яC°дA°д=1£ђ°аЄщЊЁћв“в“„µ√£Ї|x1-x2|=
£ђ
°а£®x1-x2£©2=
£ђЉі£®x1+x2£©2-4x1x2=
°а1+4b=
£ђљвµ√b=-
£Ѓ
°аx2+x+
=0£ђљвµ√x=
їтx=
£Ѓ
°яµгC°дµƒЇб„ш±кљѕіу£ђ°аx=
£Ѓ
µ±x=
±£ђy=x2=
£ђ
°аP£®
£ђ
£©£ї

Ґ№ƒж ±’л–э„™45°г£ђµгA°ҐB¬д‘Џ≈„ќпѕя…ѕ£Ѓ
“тќ™ƒж ±’л–э„™45°гЇу£ђ÷±ѕяA°дB°д”лy÷б∆љ––£ђ“тќ™”л≈„ќпѕя„оґа÷їƒ№”–“їЄцљїµг£ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
ҐЁƒж ±’л–э„™45°г£ђµгB°ҐC¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ4Ћщ Њ£Ї
”륟Ќђјн£ђњ…«уµ√£ЇP£®
£ђ
£©£ї
Ґёƒж ±’л–э„™45°г£ђµгC°ҐA¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ5Ћщ Њ£Ї
”륏Ќђјн£ђњ…«уµ√£ЇP£®
£ђ
£©£Ѓ
„џ…ѕЋщ ц£ђµгPµƒ„ш±кќ™£Ї£®0£ђ
£©£ђ£®
£ђ
£©£ђ£®
£ђ
£©£ђ£®
£ђ
£©£Ѓ
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
A1CЇЌDFµƒќї÷√єЎѕµ «∆љ––£Ѓ
£®2£©°я°чABC»∆‘≠µг∞іЋ≥ ±’лЈљѕт–э„™45°гЇуµƒ»эљ«–ќЉіќ™°чDEF£ђ
°аҐўµ±≈„ќпѕяЊ≠єэµгD°ҐE ±£ђЄщЊЁћв“вњ…µ√£Ї
|
љвµ√
|
°аy=2
| 2 |
| 2 |
ҐЏµ±≈„ќпѕяЊ≠єэµгD°ҐF ±£ђЄщЊЁћв“вњ…µ√£Ї
|
љвµ√
|
°аy=2
| 2 |
| 2 |
Ґџµ±≈„ќпѕяЊ≠єэµгE°ҐF ±£ђЄщЊЁћв“вњ…µ√£Ї
|
љвµ√
|
°аy=2
| 2 |
| 2 |
£®3£©‘Џ–э„™єэ≥ћ÷–£ђњ…ƒ№”–“‘ѕ¬«й–ќ£Ї

ҐўЋ≥ ±’л–э„™45°г£ђµгA°ҐB¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ1Ћщ Њ£Ї
“„«уµ√µгP„ш±кќ™£®0£ђ
1-
| ||
| 2 |
ҐЏЋ≥ ±’л–э„™45°г£ђµгB°ҐC¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ2Ћщ Њ£Ї
…иµгB°д£ђC°дµƒЇб„ш±кЈ÷±рќ™x1£ђx2£Ѓ
“„÷™іЋ ±B°дC°д”л“ї°Ґ»эѕуѕёљ«∆љЈ÷ѕя∆љ––£ђ°а…и÷±ѕяB°дC°дµƒљвќц љќ™y=x+b£ђ
Ѕ™ЅҐy=x2”лy=x+bµ√£Їx2=x+b£ђЉіx2-x-b=0£ђ
°аx1+x2=1£ђx1x2=-b£Ѓ
°яB°дC°д=1£ђ°аЄщЊЁћв“в“„µ√£Ї|x1-x2|=
| ||
| 2 |
°а£®x1-x2£©2=
| 1 |
| 2 |
| 1 |
| 2 |
°а1+4b=
| 1 |
| 2 |
| 1 |
| 8 |
°аx2-x+
| 1 |
| 8 |
2+
| ||
| 4 |
2-
| ||
| 4 |
°яµгC°дµƒЇб„ш±кљѕ–°£ђ°аx=
2-
| ||
| 4 |
µ±x=
2-
| ||
| 4 |
3-2
| ||
| 8 |
°аP£®
2-
| ||
| 4 |
3-2
| ||
| 8 |
ҐџЋ≥ ±’л–э„™45°г£ђµгC°ҐA¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ3Ћщ Њ£Ї
…иµгC°д£ђA°дµƒЇб„ш±кЈ÷±рќ™x1£ђx2£Ѓ
“„÷™іЋ ±C°дA°д”лґю°ҐЋƒѕуѕёљ«∆љЈ÷ѕя∆љ––£ђ°а…и÷±ѕяC°дA°дµƒљвќц љќ™y=-x+b£ђ
Ѕ™ЅҐy=x2”лy=-x+bµ√£Їx2=-x+b£ђЉіx2+x-b=0£ђ
°аx1+x2=-1£ђx1x2=-b£Ѓ
°яC°дA°д=1£ђ°аЄщЊЁћв“в“„µ√£Ї|x1-x2|=
| ||
| 2 |
°а£®x1-x2£©2=
| 1 |
| 2 |
| 1 |
| 2 |
°а1+4b=
| 1 |
| 2 |
| 1 |
| 8 |
°аx2+x+
| 1 |
| 8 |
| ||
| 4 |
-
| ||
| 4 |
°яµгC°дµƒЇб„ш±кљѕіу£ђ°аx=
| ||
| 4 |
µ±x=
| ||
| 4 |
3-2
| ||
| 8 |
°аP£®
| ||
| 4 |
3-2
| ||
| 8 |

Ґ№ƒж ±’л–э„™45°г£ђµгA°ҐB¬д‘Џ≈„ќпѕя…ѕ£Ѓ
“тќ™ƒж ±’л–э„™45°гЇу£ђ÷±ѕяA°дB°д”лy÷б∆љ––£ђ“тќ™”л≈„ќпѕя„оґа÷їƒ№”–“їЄцљїµг£ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
ҐЁƒж ±’л–э„™45°г£ђµгB°ҐC¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ4Ћщ Њ£Ї
”륟Ќђјн£ђњ…«уµ√£ЇP£®
| ||
| 4 |
3-2
| ||
| 8 |
Ґёƒж ±’л–э„™45°г£ђµгC°ҐA¬д‘Џ≈„ќпѕя…ѕ£ђ»зірЌЉ5Ћщ Њ£Ї
”륏Ќђјн£ђњ…«уµ√£ЇP£®
2+
| ||
| 4 |
3+2
| ||
| 8 |
„џ…ѕЋщ ц£ђµгPµƒ„ш±кќ™£Ї£®0£ђ
1-
| ||
| 2 |
2-
| ||
| 4 |
3-2
| ||
| 8 |
| ||
| 4 |
3-2
| ||
| 8 |
2+
| ||
| 4 |
3+2
| ||
| 8 |
µг∆ј£Ї±ЊћвњЉ≤йЅЋ–э„™±дїї”лґюіќЇѓ эµƒ„џЇѕћв–Ќ£ђƒ—ґ»љѕіу£ЃµЏ£®3£©ќ «±Њћвƒ—µгЋщ‘Џ£ђљвћвєЎЉь «£ЇµЏ“ї£ђ–э„™Јљѕт”–Ѕљ÷÷њ…ƒ№£ђ¬д‘Џ≈„ќпѕя…ѕµƒµг”–»э÷÷њ…ƒ№£ђ“тіЋє≤”–Ѕщ÷÷њ…ƒ№µƒ«й–ќ£ђ–и“™Ј÷јаћ÷¬џ£їµЏґю£ђ’лґ‘√њ“ї÷÷њ…ƒ№µƒ«й–ќ£ђ∞і’’–э„™Јљѕт”л–э„™љ«ґ»£ђ»Јґ®ЌЉ–ќ–ќ„і≤Ґљш––Љ∆Ћг£Ѓ

ЅЈѕ∞≤бѕµЅ–ір∞Є
ѕаєЎћвƒњ
 £®2013•“еќЏ –£©»зЌЉ£ђ÷±ѕяa°ќb£ђ÷±ѕяc”лa£ђbѕаљї£ђ°ѕ1=55°г£ђ‘т°ѕ2=£®°°°°£©
£®2013•“еќЏ –£©»зЌЉ£ђ÷±ѕяa°ќb£ђ÷±ѕяc”лa£ђbѕаљї£ђ°ѕ1=55°г£ђ‘т°ѕ2=£®°°°°£©