Question

【题目】如图，二次函数的图像与轴交于，两点，其中点，，点都在抛物线上，为抛物线的顶点.

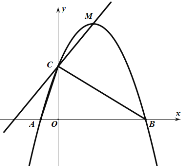
（1）求抛物线的函数解析式；

（2）求直线的解析式；

（3）求的面积.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）A（-1，0），C（0，5），D（1，8）代入y=ax2+bx+c得到关于a、b、c的方程组，解方程组求出a、b、c的值即可得到二次函数解析式；
（2）先把抛物线解析式配成顶点式，则可确定M点坐标为（2，9），软件利用待定系数法确定直线CM的解析式；
（3）先确定直线CM与x轴的交点D的坐标和抛物线与x轴的交点B的坐标，然后利用S△MCB=S△MBE-S△CBE进行计算．

（1）根据题意得，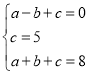

解得，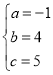

所以二次函数解析式为；

（2）如图：

，

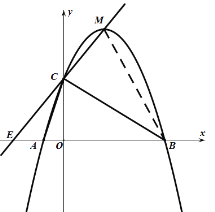
则点坐标为，

设直线的解析式为，

把和代入得，

解得，

所以直线的解析式为；

（3）把代入得，

解得，

则点坐标为，

把代入得，

解得，，

所以.