题目内容
 如图,已知点A是一次函数y=
如图,已知点A是一次函数y=| 3 |
| k |
| x |
| ||
| 2 |
A、
| ||
B、2
| ||
C、2
| ||
| D、4 |
分析:先根据△AOB的面积求出k的值进而求出反比例函数的解析式,根据正比例函数与反比例函数有交点可求出A点坐标,利用两点间的距离公式可求出OC的长,由OA=OC可求出C点的坐标,再利用两点间的距离公式即可解答.
解答:解:∵A点在反比例函数y=
的图象上,
∴设A点的横坐标为x,则纵坐标为
,
∵△AOB的面积为
,即
x•
=
=
,
∴k=
,
∴此反比例函数的解析式为y=
,
∵一次函数y=
x的图象与反比例函数y=
的图象在第一象限内的交点,
∴
x=
,
∴x=1或x=-1(舍去),
∴A点坐标为(1,
),
∴OA=
=2,
∵OA=OC,
∴C点坐标为(-2,0),
∴AC=
=2
.
故选B.
| k |
| x |
∴设A点的横坐标为x,则纵坐标为
| k |
| x |
∵△AOB的面积为
| ||
| 2 |
| 1 |
| 2 |
| k |
| x |
| k |
| 2 |
| ||
| 2 |
∴k=
| 3 |
∴此反比例函数的解析式为y=
| ||
| x |
∵一次函数y=
| 3 |
| ||
| x |
∴
| 3 |
| ||
| x |
∴x=1或x=-1(舍去),
∴A点坐标为(1,
| 3 |
∴OA=
12+(
|
∵OA=OC,
∴C点坐标为(-2,0),
∴AC=
(-2-1)2+(
|
| 3 |
故选B.
点评:本题考查的是反比例函数图象上点的坐标特点及两点之间的距离公式、用待定系数法求反比例函数的解析式、各象限内点的坐标特点,难度适中.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
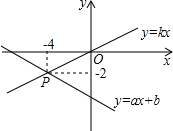 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线上的概率是( )
六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线上的概率是( ) 你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么?
你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么? 如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组
如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组