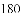��Ŀ����
ij���ڵ�����ʵʩ������ƶ�����ߵĺ����£�������չ�Ƽ���ƶ����������ũ���齨ũ����Ʒ���۹�˾��ijũ����Ʒ�������������100������ò�Ʒ����������y����Ԫ���������x�������֮��ĺ���ͼ���Ƕ���Ϊԭ��������ߵ�һ���֣���ͼ����ʾ�����ò�Ʒ�����۵���z��Ԫ/��������������x�������֮��ĺ���ͼ������ͼ����ʾ��һ���߶Σ��������IJ�Ʒ�����ڵ��������꣬�ﵽ����ƽ�⣬����ë����Ϊw��Ԫ����ë����=���۶�������ã�
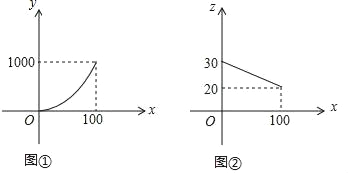
��1����ֱ��д��y��x�Լ�z��x֮��ĺ�����ϵʽ��
��2����w��x֮��ĺ�����ϵʽ������������������ʱ������ë����������ë�����Ƕ��٣�
��3���������ʽ��Ӱ�죬����Ͷ�������ķ��ò��ᳬ��360��Ԫ���������ɻ�ö�����Ԫ��ë����
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�ij��˾����һ�����ͽ��ܵ�ˮ�����������ۣ������ڼ׳��к��ҳ���������ͬ�ط�����ͬ���۷����������ۣ��Ա㿪���г���
��ֻ�ڼ׳������ۣ����ۼ۸�Ϊ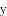
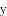
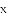
������ |
|
|
���ۼ۸� |
|
|
�ɱ�Ϊ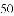
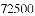
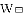 ��Ԫ��
��Ԫ��
������
��ֻ���ҳ������ۣ����ۼ۸�Ϊ
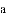
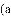
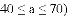
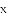
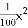 Ԫ�ĸ��ӷѣ���������Ϊ
Ԫ�ĸ��ӷѣ���������Ϊ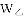 ��Ԫ��������
��Ԫ��������
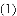
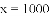
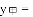 ________Ԫ/����
________Ԫ/����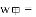 ________Ԫ��
________Ԫ��
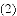
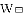 ��
��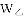 ��
��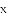
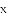
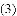
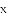
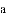
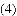
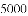


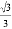 x�ϣ����A2018������Ϊ��������
x�ϣ����A2018������Ϊ��������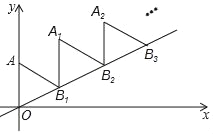
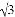 ��2020�� B. ��2018
��2020�� B. ��2018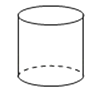 B.
B. 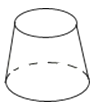 C.
C. 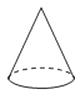 D.
D. 
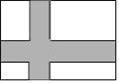
 �����ѽ⼯�������ϱ�ʾ������
�����ѽ⼯�������ϱ�ʾ������
 B.
B.  C.
C.  D.
D.