题目内容
已知△ABC的某两个内角的比是4:7且AB=AC,BD⊥AC于D,BE平分∠ABC交AC于E,则∠EBD的大小是________或________.
15° 18°
分析:根据三角形内角和定理求得各角的度数(注意分两种情况进行分析),再根据角平分线的性质及三角形内角和定理分别求得∠ABE与∠ABD的度数,从而不难求解.
解答:①如图1,当三个内角的比为:4:4:7时,三个内角分别是48°,48°,84°.
∵BE平分∠ABC,BD⊥AC,∠A=84°,
∴∠ABE= ∠ABC=24°,∠ABD=90°-84°=6°,
∠ABC=24°,∠ABD=90°-84°=6°,
∴∠EBD=∠ABE-∠ABD=24°-6°=18°.
②如图2,当三个内角的比为:4:7:7时,三个内角分别是40°,70°,70°.
∵BE平分∠ABC,BD⊥AC,∠A=40°,
∴∠ABE= ∠ABC=35°,∠ABD=90°-40°=50°,
∠ABC=35°,∠ABD=90°-40°=50°,
∴∠EBD=∠ABD-∠ABE=50°-35°=15°.
故答案为:18°,15°

点评:此题主要考查等腰三角形的性质及三角形内角和定理的综合运用.
分析:根据三角形内角和定理求得各角的度数(注意分两种情况进行分析),再根据角平分线的性质及三角形内角和定理分别求得∠ABE与∠ABD的度数,从而不难求解.
解答:①如图1,当三个内角的比为:4:4:7时,三个内角分别是48°,48°,84°.
∵BE平分∠ABC,BD⊥AC,∠A=84°,
∴∠ABE=
 ∠ABC=24°,∠ABD=90°-84°=6°,
∠ABC=24°,∠ABD=90°-84°=6°,∴∠EBD=∠ABE-∠ABD=24°-6°=18°.
②如图2,当三个内角的比为:4:7:7时,三个内角分别是40°,70°,70°.
∵BE平分∠ABC,BD⊥AC,∠A=40°,
∴∠ABE=
 ∠ABC=35°,∠ABD=90°-40°=50°,
∠ABC=35°,∠ABD=90°-40°=50°,∴∠EBD=∠ABD-∠ABE=50°-35°=15°.
故答案为:18°,15°

点评:此题主要考查等腰三角形的性质及三角形内角和定理的综合运用.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
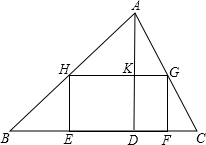
元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.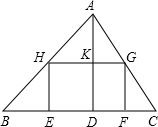 如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,种草的面积与种花的面积相等?
如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,种草的面积与种花的面积相等?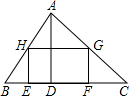 如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,喷泉面积恰好等于锐角三角形ABC的一半,并求出此时种草的面积和种花的面积各是多少平方米?
如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,喷泉面积恰好等于锐角三角形ABC的一半,并求出此时种草的面积和种花的面积各是多少平方米?