Question

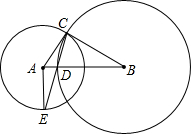
如图，△ABO中，OA=OB，以O为圆心的圆经过AB的中点C，且分别交OA、OB于点E、F．
（1）求证：AB是⊙O的切线；
（2）若△ABO腰上的高等于底边的一半，且AB=4

3

，求

ECF

的长．

Answer 1

（1）证明：连接OC．（1分）
∵OA=OB，AC=BC，
∴OC⊥AB．
∵C在⊙O上，
∴AB是⊙O的切线．（2分）

（2）过B点作BD⊥AO，交AO的延长线于D点．
由题意有AB=2BD，AB=4

3

．
在Rt△ABD中，根据正弦定义sinA=

BD

AB

=

1

2

，
∴∠A=30度．（3分）
在Rt△ACO中，AC=

1

2

AB=2

3

，∠A=30°，
则AO=2OC．
由勾股定理，求得OC=2．（4分）
∵OA=OB，且∠A=30°，
∴∠AOB=120度．
由弧长公式可求得

ECF

的长为

4

3

π．（5分）