题目内容
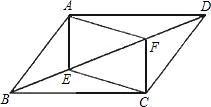
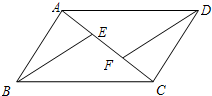 如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
分析:运用平行四边形的性质得到相关的线段、角相等,从而证明两个三角形全等.
解答: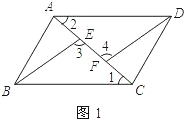 解:猜想:BE∥DF,BE=DF.
解:猜想:BE∥DF,BE=DF.
证明:
证法一:如图1
∵四边形ABCD是平行四边形,
∴BC=AD,∠1=∠2,
又∵CE=AF,
∴△BCE≌△DAF.
∴BE=DF,∠3=∠4.
∴BE∥DF.
证法二:如图2
连接BD,交AC于点O,连接DE,BF,
∵四边形ABCD是平行四边形,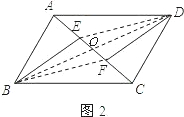
∴BO=OD,AO=CO,
又∵AF=CE,
∴AE=CF.
∴EO=FO.
∴四边形BEDF是平行四边形.
∴BE
DF.
 解:猜想:BE∥DF,BE=DF.
解:猜想:BE∥DF,BE=DF.证明:
证法一:如图1
∵四边形ABCD是平行四边形,
∴BC=AD,∠1=∠2,
又∵CE=AF,
∴△BCE≌△DAF.
∴BE=DF,∠3=∠4.
∴BE∥DF.
证法二:如图2
连接BD,交AC于点O,连接DE,BF,
∵四边形ABCD是平行四边形,

∴BO=OD,AO=CO,
又∵AF=CE,
∴AE=CF.
∴EO=FO.
∴四边形BEDF是平行四边形.
∴BE
| ∥ |
. |
点评:本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 8、
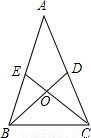
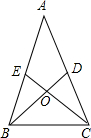
8、 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
 相交于点C.
相交于点C.
 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.