Question

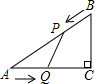
如图，在Rt△ACB中，∠ACB=90°，点O在AB上，且CA=CO=6，cos∠CAB=，若将△ACB绕点A顺时针旋转得到Rt△AC′B′，且C′落在CO的延长线上，连接BB′交CO的延长线于点F，则BF=________．

Answer 1

14
分析：过C作CD⊥AB于点D，根据等腰三角形三线合一的性质可得AD=DO，然后根据∠CAB的余弦值列式求出AB、AD的值，再求出AO的值，根据BO=AB-AO代入数据求出BO，然后根据旋转的性质可得AC=AC′，AB=AB′，再根据旋转角得到∠CAC′=∠BAB′，然后根据三角形的内角和定理求出∠ABB′=∠ACC′，从而求出∠BOF=∠BFO，根据等角对等边的性质可得BF=BO，从而得解．
解答：解：过C作CD⊥AB于点D，
∵CA=CO，
∴AD=DO，
在Rt△ACB中，cos∠CAB===，
∴AB=3AC=18，
在Rt△ADC中：cos∠CAB==，
∴AD=AC=2，
∴AO=2AD=4，
∴BO=AB-AO=18-4=14，
∵△AC′B′是由△ACB旋转得到，
∴AC=AC′，AB=AB′，∠CAC′=∠BAB′，
∵∠ACC′=（180°-∠CAC′），∠ABB′=（180°-∠BAB′），
∴∠ABB′=∠ACC′，
∴在△CAO和△BFO中，∠BFO=∠CAO，
∵CA=CO，
∴∠COA=∠CAO，
又∵∠COA=∠BOF（对顶角相等），
∴∠BOF=∠BFO，
∴BF=BO=14．
故答案为：14．
点评：本题考查了旋转的性质，等腰三角形三线合一的性质，三角形的内角和定理，以及锐角三角函数的应用，求出BO的长度之后，难点在于求BF=BO．