��Ŀ����
��2004•��������ͼ��ֱ��l��y=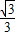 x+
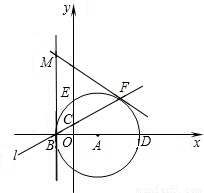
x+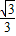 ��x�ᡢy��ֱ��ڵ�B��C���Ե�A��1��0��ΪԲ�ģ���AB�ij�Ϊ�뾶����A���ֱ�x�ᡢy���������ڵ�D��E��ֱ��l���A���ڵ�F���ֱ����B��F����A�����߽��ڵ�M��
��x�ᡢy��ֱ��ڵ�B��C���Ե�A��1��0��ΪԲ�ģ���AB�ij�Ϊ�뾶����A���ֱ�x�ᡢy���������ڵ�D��E��ֱ��l���A���ڵ�F���ֱ����B��F����A�����߽��ڵ�M����1��ֱ��д����B��C�����ꣻ
��2����ֱ��MF�Ľ���ʽ��
��3������P��
 ������һ�㣨����B��F�غϣ�������BP��FP������M��MN��PF����ֱ��l�ڵ�N����PB=a��MN=b����b��a�ĺ�����ϵʽ����д���Ա���a��ȡֵ��Χ��
������һ�㣨����B��F�غϣ�������BP��FP������M��MN��PF����ֱ��l�ڵ�N����PB=a��MN=b����b��a�ĺ�����ϵʽ����д���Ա���a��ȡֵ��Χ����4��������3���е�������P��
 ������һ�㣬��Ϊ��P�ǡ�A������һ�㣬�����������䣮����P�ڡ�A�ϵ�ʲôλ��ʱ����BMNΪֱ�������Σ���д����ʱ��N�����꣮���ڣ�4����ֱ��д���������Ҫ��֤���������̣�
������һ�㣬��Ϊ��P�ǡ�A������һ�㣬�����������䣮����P�ڡ�A�ϵ�ʲôλ��ʱ����BMNΪֱ�������Σ���д����ʱ��N�����꣮���ڣ�4����ֱ��д���������Ҫ��֤���������̣�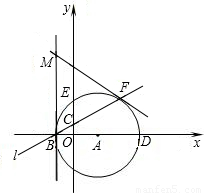
���𰸡���������1���ֱ���x=0��y=0�������B��C�����ꣻ
��2������AH��BF��H��FG��BD��G������tan��CBO�����CBO=30°����Բ�İ뾶AB=2������HA= AB=1��BH=
AB=1��BH= ��������������BF=2
��������������BF=2 ������FG=
������FG= BF=
BF= BC=3OG=2������F��2��
BC=3OG=2������F��2�� ���������MBF=60°��BM=MF����֪MB=MF=BF=2
���������MBF=60°��BM=MF����֪MB=MF=BF=2 ��M��-1��2
��M��-1��2 ��������ֱ��MF�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ֱ�ߵĽ���ʽ��
��������ֱ��MF�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ֱ�ߵĽ���ʽ��
��3����ΪMN��PF�����ԡ�NMF=��PFM�������PFM=��PBF�����ԡ�PBF=��FMN��������֤��PBF�ס�FMN������ ������������ݣ��������a��b�Ĺ�ϵʽ����0��a��2
������������ݣ��������a��b�Ĺ�ϵʽ����0��a��2 ��
��
��4����Ϊ����P���E�����D�غ�ʱ����BMNΪֱ�������Σ����Դ�ʱ��N����Ϊ��5��2 ������
������ ����
����
����⣺��1��B��-1��0����C��0�� ����
����
��2����AH��BF��H��FG��BD��G��
 tan��CBO=
tan��CBO= =
= ��
��
���CBO=30°
��HA= AB=1��
AB=1��
��BH= ��BF=2BH=2
��BF=2BH=2 ��
��
��FG= BF=
BF= ��BC=3OG=2��
��BC=3OG=2��
��F��2�� ����
����
�ߡ�MBF=60°��BM=MF��
��MB=MF=BF=2 ��
��
��M��-1��2 ����
����
��ֱ��MF�Ľ���ʽΪy=kx+b��
�� ��
��
�� ��
��
��y=- x+
x+ y��
y��
��3����MN��PF��
���NMF=��PFM��
�ߡ�PFM=��PBF��
���PBF=��FMN��
�ߡ�MNF=��BFP��
���PBF�ס�FMN��
�� ��
��
�� ��
��
��ab=12��
��b= ��
��
0��a��2 ��
��
��4������P���E�����D�غ�ʱ����BMNΪֱ�������Σ�
��ʱ��N����Ϊ��5��2 ������
������ ����
����
��������������ϸ�������⣬�������������ε����ʺ�Բ���й�֪ʶ���ɽ�����⣮
��2������AH��BF��H��FG��BD��G������tan��CBO�����CBO=30°����Բ�İ뾶AB=2������HA=
 AB=1��BH=
AB=1��BH= ��������������BF=2
��������������BF=2 ������FG=
������FG= BF=
BF= BC=3OG=2������F��2��
BC=3OG=2������F��2�� ���������MBF=60°��BM=MF����֪MB=MF=BF=2
���������MBF=60°��BM=MF����֪MB=MF=BF=2 ��M��-1��2
��M��-1��2 ��������ֱ��MF�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ֱ�ߵĽ���ʽ��
��������ֱ��MF�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ֱ�ߵĽ���ʽ����3����ΪMN��PF�����ԡ�NMF=��PFM�������PFM=��PBF�����ԡ�PBF=��FMN��������֤��PBF�ס�FMN������
 ������������ݣ��������a��b�Ĺ�ϵʽ����0��a��2
������������ݣ��������a��b�Ĺ�ϵʽ����0��a��2 ��
����4����Ϊ����P���E�����D�غ�ʱ����BMNΪֱ�������Σ����Դ�ʱ��N����Ϊ��5��2
 ������
������ ����
��������⣺��1��B��-1��0����C��0��
 ����
������2����AH��BF��H��FG��BD��G��
 tan��CBO=
tan��CBO= =
= ��
�����CBO=30°
��HA=
 AB=1��
AB=1����BH=
 ��BF=2BH=2
��BF=2BH=2 ��
����FG=
 BF=
BF= ��BC=3OG=2��
��BC=3OG=2����F��2��
 ����
�����ߡ�MBF=60°��BM=MF��
��MB=MF=BF=2
 ��
����M��-1��2
 ����
������ֱ��MF�Ľ���ʽΪy=kx+b��
��
 ��
����
 ��
����y=-
 x+
x+ y��
y����3����MN��PF��
���NMF=��PFM��
�ߡ�PFM=��PBF��
���PBF=��FMN��
�ߡ�MNF=��BFP��
���PBF�ס�FMN��
��
 ��
����
 ��
����ab=12��
��b=
 ��
��0��a��2
 ��
����4������P���E�����D�غ�ʱ����BMNΪֱ�������Σ�
��ʱ��N����Ϊ��5��2
 ������
������ ����
������������������ϸ�������⣬�������������ε����ʺ�Բ���й�֪ʶ���ɽ�����⣮

��ϰ��ϵ�д�
 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
�����Ŀ
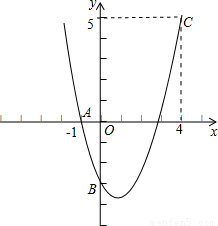
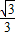 x+
x+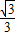 ��x�ᡢy��ֱ��ڵ�B��C���Ե�A��1��0��ΪԲ�ģ���AB�ij�Ϊ�뾶����A���ֱ�x�ᡢy���������ڵ�D��E��ֱ��l���A���ڵ�F���ֱ����B��F����A�����߽��ڵ�M��
��x�ᡢy��ֱ��ڵ�B��C���Ե�A��1��0��ΪԲ�ģ���AB�ij�Ϊ�뾶����A���ֱ�x�ᡢy���������ڵ�D��E��ֱ��l���A���ڵ�F���ֱ����B��F����A�����߽��ڵ�M��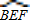 ������һ�㣨����B��F�غϣ�������BP��FP������M��MN��PF����ֱ��l�ڵ�N����PB=a��MN=b����b��a�ĺ�����ϵʽ����д���Ա���a��ȡֵ��Χ��
������һ�㣨����B��F�غϣ�������BP��FP������M��MN��PF����ֱ��l�ڵ�N����PB=a��MN=b����b��a�ĺ�����ϵʽ����д���Ա���a��ȡֵ��Χ�� ������һ�㣬��Ϊ��P�ǡ�A������һ�㣬�����������䣮����P�ڡ�A�ϵ�ʲôλ��ʱ����BMNΪֱ�������Σ���д����ʱ��N�����꣮���ڣ�4����ֱ��д���������Ҫ��֤���������̣�
������һ�㣬��Ϊ��P�ǡ�A������һ�㣬�����������䣮����P�ڡ�A�ϵ�ʲôλ��ʱ����BMNΪֱ�������Σ���д����ʱ��N�����꣮���ڣ�4����ֱ��д���������Ҫ��֤���������̣�