题目内容
计算:
(1) ;
;
(2)如果直角三角形的两直角边的长分别为 +1和
+1和 -1.求斜边c的长.
-1.求斜边c的长.
解:(1)原式=(2 -3
-3 )×
)× +3
+3
=2-3 +3
+3
=2,
(2)根据题意得方程:(2 +1)2+(2
+1)2+(2 -1)2=c2,
-1)2=c2,
整理方程得:c2=26,
解方程得:c=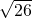 ,
,
当c=-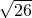 时,不符合题意,故舍去,
时,不符合题意,故舍去,
∴c=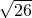 .
.
分析:(1)首先把除法转化为乘法,然后按照乘法分配原则进行乘法运算,再对每项二次根式化简后进行合并同类二次根式即可;
(2)根据勾股定理即可推出两条直角边与斜边的关系,可推出(2 +1)2+(2
+1)2+(2 -1)2=c2,然后运用完全平方公式,进行解方程即可求出斜边c的长度.
-1)2=c2,然后运用完全平方公式,进行解方程即可求出斜边c的长度.
点评:本题主要考查二次根式的化简,二次根式的混合运算,勾股定理的应用,完全平方公式的应用,关键在于正确的运用相关的运算法则,认真的进行计算.
 -3
-3 )×
)× +3
+3
=2-3
 +3
+3
=2,
(2)根据题意得方程:(2
 +1)2+(2
+1)2+(2 -1)2=c2,
-1)2=c2,整理方程得:c2=26,
解方程得:c=
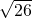 ,
,当c=-
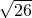 时,不符合题意,故舍去,
时,不符合题意,故舍去,∴c=
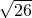 .
.分析:(1)首先把除法转化为乘法,然后按照乘法分配原则进行乘法运算,再对每项二次根式化简后进行合并同类二次根式即可;
(2)根据勾股定理即可推出两条直角边与斜边的关系,可推出(2
 +1)2+(2
+1)2+(2 -1)2=c2,然后运用完全平方公式,进行解方程即可求出斜边c的长度.
-1)2=c2,然后运用完全平方公式,进行解方程即可求出斜边c的长度.点评:本题主要考查二次根式的化简,二次根式的混合运算,勾股定理的应用,完全平方公式的应用,关键在于正确的运用相关的运算法则,认真的进行计算.

练习册系列答案
相关题目
