Question

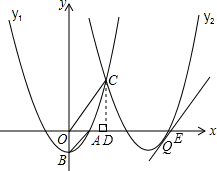
如图，抛物线y₁=x²-1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y₂，两条抛物线相交于点C．
（1）请直接写出抛物线y₂的解析式；
（2）若点P是x轴上一动点，且满足∠CPA=∠OBA，求出所有满足条件的P点坐标；
（3）在第四象限内抛物线y₂上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q的坐标及h的最大值；若不存在，请说明理由．

Answer 1

（1）抛物线y₁=x²-1向右平移4个单位的顶点坐标为（4，-1），
所以，抛物线y₂的解析式为y₂=（x-4）²-1；

（2）x=0时，y=-1，
y=0时，x²-1=0，解得x₁=1，x₂=-1，
所以，点A（1，0），B（0，-1），
∴∠OBA=45°，
联立

y=x2-1 y=(x-4)2-1

，
解得

x=2 y=3

，
∴点C的坐标为（2，3），
∵∠CPA=∠OBA，
∴点P在点A的左边时，坐标为（-1，0），
在点A的右边时，坐标为（5，0），
所以，点P的坐标为（-1，0）或（5，0）；

（3）存在．
∵点C（2，3），
∴直线OC的解析式为y=

3

2

x，
设与OC平行的直线y=

3

2

x+b，
联立

y= 3 2 x+b y=(x-4)2-1

，
消掉y得，2x²-19x+30-2b=0，
当△=0，方程有两个相等的实数根时，△QOC中OC边上的高h有最大值，
此时x₁=x₂=

1

2

×（-

-19

2

）=

19

4

，
此时y=（

19

4

-4）²-1=-

7

16

，
∴存在第四象限的点Q（

19

4

，-

7

16

），使得△QOC中OC边上的高h有最大值，
此时△=19²-4×2×（30-2b）=0，
解得b=-

121

16

，
∴过点Q与OC平行的直线解析式为y=

3

2

x-

121

16

，
令y=0，则

3

2

x-

121

16

=0，解得x=

121

24

，
设直线与x轴的交点为E，则E（

121

24

，0），
过点C作CD⊥x轴于D，根据勾股定理，OC=

22+32

=

13

，
则sin∠COD=

h

EO

=

3

13

，
解得h_最大=

3

13

×

121

24

=

121 13

104

．