题目内容
 如图,已知反比函数y=
如图,已知反比函数y= 的图象过直角三角形OAB斜边OB的中点D,与直角边AB相交于C,连结AD、OC,△OAB的周长为4
的图象过直角三角形OAB斜边OB的中点D,与直角边AB相交于C,连结AD、OC,△OAB的周长为4 +8.AD=4.下列结论:
+8.AD=4.下列结论:
①k=-1;②AC:CB=1:3;③△OBC的面积等于3; ④k=-2,其中正确的是
- A.①②③
- B.②③④
- C.①②
- D.③④
B
分析:在直角三角形AOB中,由斜边上的中线等于斜边的一半,求出OB的长,根据周长求出直角边之和,设其中一直角边AB=x,表示出OA,利用勾股定理求出AB与OA的长,求出三角形AOB的面积,过D作DE垂直于x轴,得到E为OA中点,求出OE的长,在直角三角形DOE中,利用勾股定理求出DE的长,利用反比例函数k的几何意义求出k的值,确定出三角形AOC面积,进而求出三角形BOC面积,根据两三角形高相同,得到底BC与AC之比,即可做出判断.
解答: 解:在Rt△AOB中,AD=4,AD为斜边OB的中线,
解:在Rt△AOB中,AD=4,AD为斜边OB的中线,
∴OB=2AD=8,
由周长为4 +8,得到AB+AO=4
+8,得到AB+AO=4 ,
,
设AB=x,则AO=4 -x,
-x,
根据勾股定理得:AB2+OA2=OB2,即x2+(4 -x)2=82,
-x)2=82,
整理得:x2-4 x+8=0,
x+8=0,
解得:x1=2 +2
+2 ,x2=2
,x2=2 -2
-2 ,
,
∴AB=2 +2
+2 ,OA=2
,OA=2 -2
-2 ,
,
∴S△AOB= AB•OA=
AB•OA= ×(2
×(2 +2
+2 )×(2
)×(2 -2
-2 )=4,
)=4,
过D作DE⊥x轴,交x轴于点E,可得E为AO中点,
∴OE= OA=
OA= -
- (假设OA=2
(假设OA=2 -2
-2 ,若OA=2
,若OA=2 +2
+2 ,求出结果相同),
,求出结果相同),
在Rt△DEO中,利用勾股定理得:DE=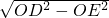 =
= +
+ ,
,
∴k=-DE•OE=-( +
+ )×(
)×( -
- )=-2,
)=-2,
∴S△COA= |k|=1,S△BCO=4-1=3,
|k|=1,S△BCO=4-1=3,
∵△BCO与△CAO同高,且面积之比为3:1,
∴BC:AC=3:1,
则其中正确的选项有②③④.
故选B
点评:此题属于反比例函数综合题,涉及的知识有:勾股定理,直角三角形斜边的中线性质,三角形面积求法,以及反比例函数k的几何意义,熟练掌握反比例的图象与性质是解本题关键.
分析:在直角三角形AOB中,由斜边上的中线等于斜边的一半,求出OB的长,根据周长求出直角边之和,设其中一直角边AB=x,表示出OA,利用勾股定理求出AB与OA的长,求出三角形AOB的面积,过D作DE垂直于x轴,得到E为OA中点,求出OE的长,在直角三角形DOE中,利用勾股定理求出DE的长,利用反比例函数k的几何意义求出k的值,确定出三角形AOC面积,进而求出三角形BOC面积,根据两三角形高相同,得到底BC与AC之比,即可做出判断.
解答:
 解:在Rt△AOB中,AD=4,AD为斜边OB的中线,
解:在Rt△AOB中,AD=4,AD为斜边OB的中线,∴OB=2AD=8,
由周长为4
 +8,得到AB+AO=4
+8,得到AB+AO=4 ,
,设AB=x,则AO=4
 -x,
-x,根据勾股定理得:AB2+OA2=OB2,即x2+(4
 -x)2=82,
-x)2=82,整理得:x2-4
 x+8=0,
x+8=0,解得:x1=2
 +2
+2 ,x2=2
,x2=2 -2
-2 ,
,∴AB=2
 +2
+2 ,OA=2
,OA=2 -2
-2 ,
,∴S△AOB=
 AB•OA=
AB•OA= ×(2
×(2 +2
+2 )×(2
)×(2 -2
-2 )=4,
)=4,过D作DE⊥x轴,交x轴于点E,可得E为AO中点,
∴OE=
 OA=
OA= -
- (假设OA=2
(假设OA=2 -2
-2 ,若OA=2
,若OA=2 +2
+2 ,求出结果相同),
,求出结果相同),在Rt△DEO中,利用勾股定理得:DE=
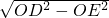 =
= +
+ ,
,∴k=-DE•OE=-(
 +
+ )×(
)×( -
- )=-2,
)=-2,∴S△COA=
 |k|=1,S△BCO=4-1=3,
|k|=1,S△BCO=4-1=3,∵△BCO与△CAO同高,且面积之比为3:1,
∴BC:AC=3:1,
则其中正确的选项有②③④.
故选B
点评:此题属于反比例函数综合题,涉及的知识有:勾股定理,直角三角形斜边的中线性质,三角形面积求法,以及反比例函数k的几何意义,熟练掌握反比例的图象与性质是解本题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数




 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数 的图象的两个交点.
的图象的两个交点.