题目内容
如图，已知点P为△ABC中∠B，∠C平分线交点，∠BPC=130°，则∠BAC=
- A.65°
- B.75°
- C.80°
- D.100°
C
∵BP、CP是∠ABC和∠ACB的角平分线，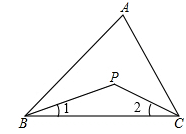
∴∠ABC=2∠1，∠ACB=2∠2，
∵∠A+∠ABC+∠ACB=180°，
∴∠A=180°-2（∠1+∠2），
∵∠1+∠2+∠P=180°，
∴∠1+∠2=180°-∠BPC =50°，
∴∠A=180°-2（∠1+∠2）=180°-2×50°=80°
故选C
∵BP、CP是∠ABC和∠ACB的角平分线，
∴∠ABC=2∠1，∠ACB=2∠2，
∵∠A+∠ABC+∠ACB=180°，
∴∠A=180°-2（∠1+∠2），
∵∠1+∠2+∠P=180°，
∴∠1+∠2=180°-∠BPC =50°，
∴∠A=180°-2（∠1+∠2）=180°-2×50°=80°
故选C
练习册系列答案
相关题目
如图，已知点C为线段AE上一点，AE=8cm，△ABC和△CDE为AE同侧的两个等边三角形，连接BE交CD于N，连接AD交BC于M，连接MN．
（2012•龙湖区模拟）如图，已知点P为反比例函数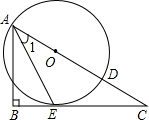
（2012•玉林）如图，已知点O为Rt△ABC斜边AC上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点E，与AC相交于点D，连接AE．
如图，已知点D为△ABC中AC边上一点，且AD：DC=3；4，设
如图，已知点D为等腰直角△ABC内一点，AC=BC，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．若DE=acm，BD=bcm（a＞b），则CD=