题目内容
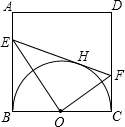
 已知,如图,正方形ABCD的对角线AC,BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
已知,如图,正方形ABCD的对角线AC,BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
(1)求证:OE=OF;
(2)若正方形ABCD的边长为1,求两个正方形重叠部分的面积;
(3)若正方形A′B′C′D′绕着点O旋转,EF的长度何时最短?(直接写答案).
(1)证明:∵正方形ABCD的对角线AC、BD交于点O
∴∠BOC=90°,∠OBC=∠OCD=∠OCF=45°,OB=OC,
∵正方形A'B'C'D'的A'B'交BC于点E,A'D'交CD于点F.
∴∠EOF=90°
∵∠BOE=∠EOF-∠EOC=90°-∠EOC
∠COF=∠BOC-∠EOC=90°-∠EOC
∴∠BOE=∠COF.
在△OBE和△OCF中,
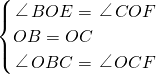 ,
,
∴△BOE≌△COF(ASA).
∴OE=OF;
(2)解:∵△BOE≌△COF,
∴S△BOE=S△COF
∴S△EOC+S△COF=S△EOC+S△BOE,
即S四边形OECF=S△BOC.
∵S△BOC= ,
,
∴两个正方形重叠部分的面积为 ;
;
(3)解:连接EF,
∵∠EOF=90°,
∴EF2=OE2+OF2.
∵OE=OF,
∴EF2=2OE2,
∴要使EF最小,则OE最小,
∴当OE垂直于BC时,OE最小= ,
,
∴EF2= ,
,
∴EF最小= .
.
分析:(1)由正方形的性质可以得出△BOE≌△COF,由全等三角形的性质就可以得出OE=OF;
(2)由全等可以得出S△BOE=S△COF,就可以得出S四边形OECF=S△BOC,S△BOC的面积就可以得出结论; (3)运用勾股定理表示出EF的表达式,当OE垂直于BC时可以求出EF 的最小值.
点评:本题考查了正方形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,解答时证明三角形全等得出OE=OF是关键.
∴∠BOC=90°,∠OBC=∠OCD=∠OCF=45°,OB=OC,
∵正方形A'B'C'D'的A'B'交BC于点E,A'D'交CD于点F.
∴∠EOF=90°
∵∠BOE=∠EOF-∠EOC=90°-∠EOC
∠COF=∠BOC-∠EOC=90°-∠EOC
∴∠BOE=∠COF.
在△OBE和△OCF中,
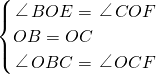 ,
,∴△BOE≌△COF(ASA).
∴OE=OF;
(2)解:∵△BOE≌△COF,
∴S△BOE=S△COF
∴S△EOC+S△COF=S△EOC+S△BOE,
即S四边形OECF=S△BOC.
∵S△BOC=
 ,
,
∴两个正方形重叠部分的面积为
 ;
;(3)解:连接EF,
∵∠EOF=90°,
∴EF2=OE2+OF2.
∵OE=OF,
∴EF2=2OE2,
∴要使EF最小,则OE最小,
∴当OE垂直于BC时,OE最小=
 ,
,∴EF2=
 ,
,∴EF最小=
 .
.分析:(1)由正方形的性质可以得出△BOE≌△COF,由全等三角形的性质就可以得出OE=OF;
(2)由全等可以得出S△BOE=S△COF,就可以得出S四边形OECF=S△BOC,S△BOC的面积就可以得出结论; (3)运用勾股定理表示出EF的表达式,当OE垂直于BC时可以求出EF 的最小值.
点评:本题考查了正方形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,解答时证明三角形全等得出OE=OF是关键.

练习册系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.



 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.