Question

【题目】如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（ ）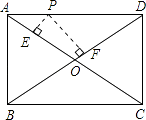

A.
B.
C.
D.不确定

Answer 1

【答案】A
【解析】解：连接OP，

∵矩形的两条边AB、BC的长分别为和4，

∴S矩形ABCD=ABBC=12，OA=OC，OB=OD，AC=BD=5，

∴OA=OD=2.5，

∴S△ACD= S矩形ABCD=6，

∴S△AOD= S△ACD=3，

∵S△AOD=S△AOP+S△DOP= OAPE+ ODPF= ×2.5×PE+ ×2.5×PF= （PE+PF）=3，

解得：PE+PF= ．

所以答案是：A．

【考点精析】利用三角形的面积和矩形的性质对题目进行判断即可得到答案，需要熟知三角形的面积=1/2×底×高；矩形的四个角都是直角，矩形的对角线相等．