题目内容
已知x为实数,且|3x-1|+|4x-1|+|5x-1|+…+|17x-1|的值是一个确定的常数,则这个常数是
- A.5
- B.10
- C.15
- D.75
A
分析:将|3x-1|+|4x-1|+|5x-1|+…+|17x-1|按照取值范围进行讨论.
解答:(1)当x> 时,原式=150x-15,不是常数;
时,原式=150x-15,不是常数;
(2)当 <x≤
<x≤ 时,原式=144x-13,不是常数;
时,原式=144x-13,不是常数;
(3)当 <x≤
<x≤ 时,原式=136x-11,不是常数;
时,原式=136x-11,不是常数;
(4)当 <x≤
<x≤ 时,原式=126x-9,不是常数;
时,原式=126x-9,不是常数;
(5)当 <x≤
<x≤ 时,原式=114x-7,不是常数;
时,原式=114x-7,不是常数;
(6)当 <x≤
<x≤ 时,原式=100x-5,不是常数;
时,原式=100x-5,不是常数;
(7)当 <x≤
<x≤ 时,原式=84x-3,不是常数;
时,原式=84x-3,不是常数;
(8)当 <x≤
<x≤ 时,原式=66x-1,不是常数;
时,原式=66x-1,不是常数;
(9)当 <x≤
<x≤ 时,原式=46x+1,不是常数;
时,原式=46x+1,不是常数;
(10)当 <x≤
<x≤ 时,原式=24x+3,不是常数;
时,原式=24x+3,不是常数;
(11)当 <x≤
<x≤ 时,原式=5,是常数;
时,原式=5,是常数;
(12)当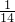 <x≤
<x≤ 时,原式=-26x+7,不是常数;
时,原式=-26x+7,不是常数;
(13)当 <x≤
<x≤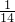 时,原式=-54x+9,不是常数;
时,原式=-54x+9,不是常数;
(14)当 <x≤
<x≤ 时,原式=-84x+11,不是常数;
时,原式=-84x+11,不是常数;
(15)当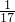 <x≤
<x≤ 时,原式=-116x+13,不是常数;
时,原式=-116x+13,不是常数;
(16)当x≤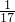 时,原式=-84x+11,不是常数.
时,原式=-84x+11,不是常数.
故选A.
点评:解答此题,要弄清绝对值的性质,分类讨论的思想.
分析:将|3x-1|+|4x-1|+|5x-1|+…+|17x-1|按照取值范围进行讨论.
解答:(1)当x>
 时,原式=150x-15,不是常数;
时,原式=150x-15,不是常数;(2)当
 <x≤
<x≤ 时,原式=144x-13,不是常数;
时,原式=144x-13,不是常数;(3)当
 <x≤
<x≤ 时,原式=136x-11,不是常数;
时,原式=136x-11,不是常数;(4)当
 <x≤
<x≤ 时,原式=126x-9,不是常数;
时,原式=126x-9,不是常数;(5)当
 <x≤
<x≤ 时,原式=114x-7,不是常数;
时,原式=114x-7,不是常数;(6)当
 <x≤
<x≤ 时,原式=100x-5,不是常数;
时,原式=100x-5,不是常数;(7)当
 <x≤
<x≤ 时,原式=84x-3,不是常数;
时,原式=84x-3,不是常数;(8)当
 <x≤
<x≤ 时,原式=66x-1,不是常数;
时,原式=66x-1,不是常数;(9)当
 <x≤
<x≤ 时,原式=46x+1,不是常数;
时,原式=46x+1,不是常数;(10)当
 <x≤
<x≤ 时,原式=24x+3,不是常数;
时,原式=24x+3,不是常数;(11)当
 <x≤
<x≤ 时,原式=5,是常数;
时,原式=5,是常数;(12)当
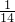 <x≤
<x≤ 时,原式=-26x+7,不是常数;
时,原式=-26x+7,不是常数;(13)当
 <x≤
<x≤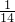 时,原式=-54x+9,不是常数;
时,原式=-54x+9,不是常数;(14)当
 <x≤
<x≤ 时,原式=-84x+11,不是常数;
时,原式=-84x+11,不是常数;(15)当
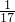 <x≤
<x≤ 时,原式=-116x+13,不是常数;
时,原式=-116x+13,不是常数;(16)当x≤
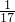 时,原式=-84x+11,不是常数.
时,原式=-84x+11,不是常数.故选A.
点评:解答此题,要弄清绝对值的性质,分类讨论的思想.

练习册系列答案
相关题目
已知x为实数,且
-(x2+3x)=2,则x2+3x的值为( )
| 3 |
| x2+3x |
| A、1 | B、1或-3 |
| C、-3 | D、-1或3 |