题目内容
 已知一次函数的图象经过点A(1,1),B(-2,7),C(m,-3).
已知一次函数的图象经过点A(1,1),B(-2,7),C(m,-3).(1)求这个一次函数的解析式;
(2)作出该函数图象;
(3)设该函数图象与y轴交于D点,O是坐标原点,求△DOC的面积.
分析:(1)设这个一次函数的解析式为y=kx+b(k、b是常数,且k≠0).把点A、B的坐标分别代入函数解析式,列出关于系数k、b的方程组,通过解方程组来求它们的值;
(2)利用“两点确定一条直线”作出图象;
(3)根据解析式求得点C、D的坐标,然后由三角形的面积公式求得△DOC的面积.
(2)利用“两点确定一条直线”作出图象;
(3)根据解析式求得点C、D的坐标,然后由三角形的面积公式求得△DOC的面积.
解答: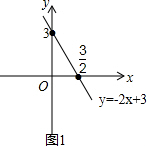 解:(1)设这个一次函数的解析式为y=kx+b(k、b是常数,且k≠0).
解:(1)设这个一次函数的解析式为y=kx+b(k、b是常数,且k≠0).
由题意得,
,
解之得
故该一次函数的解析式为y=-2x+3;
(2)由(1)知,一次函数的解析式为y=-2x+3,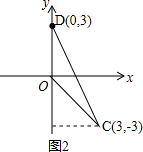
则当x=0时,y=3;当y=0时,x=
,
所以,其图象如图1所示:
(3)由(2)知,D(0,3).则OD=3.
∵点C在一次函数y=-2x+3上,
∴-3=-2m+3,
解得,m=3,
∴C(3,-3),
∴S△DOC=
OD•|yC|=
×3×3=
,即△DOC的面积是
.
 解:(1)设这个一次函数的解析式为y=kx+b(k、b是常数,且k≠0).
解:(1)设这个一次函数的解析式为y=kx+b(k、b是常数,且k≠0).由题意得,
|
解之得
|
故该一次函数的解析式为y=-2x+3;
(2)由(1)知,一次函数的解析式为y=-2x+3,

则当x=0时,y=3;当y=0时,x=
| 3 |
| 2 |
所以,其图象如图1所示:
(3)由(2)知,D(0,3).则OD=3.
∵点C在一次函数y=-2x+3上,
∴-3=-2m+3,
解得,m=3,
∴C(3,-3),
∴S△DOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
点评:本题考查了待定系数法求一次函数解析式,一次函数图象.函数与y轴的交点的横坐标为0.函数与x轴的交点的纵坐标为0.

练习册系列答案
相关题目
 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标; 和反比例函数
和反比例函数 ,求这两个函数图象在同一坐标系内的交点坐标。
,求这两个函数图象在同一坐标系内的交点坐标。
 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标;