题目内容
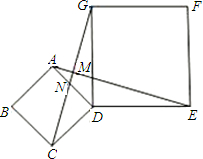
如图，已知四边形ABCD是四个角都是直角，四条边都相等的正方形，点E在BC上，且CE=
BC，点F是CD的中点，延长AF与BC的延长线交于点M．以下结论：①AB=CM；②AE=AB+CE；③S△AEF=
S四边形ABCF；④∠AFE=90°，其中正确的结论的个数有（ ）
| 1 |
| 4 |
| 1 |
| 4 |
| A．1个 | B．2个 | C．3个 | D．4个 |
由题意知，∵点F是CD的中点，∴DF=CF，
又∵∠D=∠FCM，∠DFA=∠CFM，
∴△ADF≌△MCF，
∴CM=AD=AB，
①正确；
设正方形ABCD边长为4，
∵CE=
BC=1，
∴BE=3，
∴AE=5，
∴AE=AB+CE，
②正确；
EM=CM+CE=5=AE，
又∵F为AM的中点，
∴EF⊥AM，
④正确，
由CF=2，CE=1得EF=
，
由DF=2，AD=4得AF=2
，
∴S△AEF=5，
又S△ADF=4，
∴S四边形ABCF=S□ABCD-S△ADF=12，
③不正确，
故正确的有3个，选C．
又∵∠D=∠FCM，∠DFA=∠CFM，
∴△ADF≌△MCF，
∴CM=AD=AB，
①正确；
设正方形ABCD边长为4，
∵CE=
| 1 |
| 4 |
∴BE=3，
∴AE=5，
∴AE=AB+CE，
②正确；
EM=CM+CE=5=AE，
又∵F为AM的中点，
∴EF⊥AM，
④正确，
由CF=2，CE=1得EF=
| 5 |
由DF=2，AD=4得AF=2
| 5 |
∴S△AEF=5，
又S△ADF=4，
∴S四边形ABCF=S□ABCD-S△ADF=12，
③不正确，
故正确的有3个，选C．
练习册系列答案
相关题目
点P，连接OP，OQ；
