题目内容
 如图,在⊙O中,∠AOB=120°,PT与⊙O切于T点,A、B、P共线,∠APT的平分线依次交AT、BT于C、D,求证:△ACD∽△CDB.
如图,在⊙O中,∠AOB=120°,PT与⊙O切于T点,A、B、P共线,∠APT的平分线依次交AT、BT于C、D,求证:△ACD∽△CDB.
证明:在△TCD中,∠TCD=∠TAP+∠CPA=∠BTP+∠CPT=∠CDT,
又∵∠ATB= ∠AOB=60°,
∠AOB=60°,
∴△TCD为等边三角形,且∠ACD=∠BDC,
∵PT为圆O的切线,
∴ =
= =
=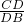 ,
,
∴△ACD∽△CDB.
分析:易证∠TCD=∠TAP+∠CPA=∠BTP+∠CPT=∠CDT,进而判定△TCD为等边三角形,进而求证 =
= =
=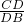 ,根据对应边比值相等可以判定△ACD∽△CPB即可解题.
,根据对应边比值相等可以判定△ACD∽△CPB即可解题.
点评:本题考查了等边三角形的判定和等边三角形各内角相等、各边长相等的性质,相似三角形的判定,本题中求证 =
= =
=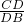 是解题的关键.
是解题的关键.
又∵∠ATB=
 ∠AOB=60°,
∠AOB=60°,∴△TCD为等边三角形,且∠ACD=∠BDC,
∵PT为圆O的切线,
∴
 =
= =
=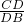 ,
,∴△ACD∽△CDB.
分析:易证∠TCD=∠TAP+∠CPA=∠BTP+∠CPT=∠CDT,进而判定△TCD为等边三角形,进而求证
 =
= =
=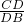 ,根据对应边比值相等可以判定△ACD∽△CPB即可解题.
,根据对应边比值相等可以判定△ACD∽△CPB即可解题.点评:本题考查了等边三角形的判定和等边三角形各内角相等、各边长相等的性质,相似三角形的判定,本题中求证
 =
= =
=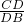 是解题的关键.
是解题的关键. 
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 19、如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明∠1=∠2,以下是证明过程,请填空:
19、如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明∠1=∠2,以下是证明过程,请填空: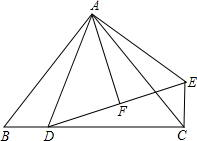 如图,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一点,EC⊥BC,EC=BD,DF=FE.求证:
如图,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一点,EC⊥BC,EC=BD,DF=FE.求证: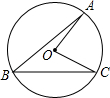 如图,在⊙O中,∠ABC=40°,则∠AOC=
如图,在⊙O中,∠ABC=40°,则∠AOC= 如图,在△ABC中,∠B,∠C的外角平分线相交于点O,若∠A=74°,则∠O=
如图,在△ABC中,∠B,∠C的外角平分线相交于点O,若∠A=74°,则∠O= 15、如图,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,则以下结论中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正确的有
15、如图,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,则以下结论中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正确的有