题目内容
在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AD,则∠B等于
- A.30°
- B.45°
- C.60°
- D.135°
B
分析:过点D作DF⊥BC于点F,已知AD=AF,AE⊥BC,DF⊥BC,从而可判定四边形AEFD为正方形,根据已知及正方形的性质可得到BE=AE,从而求得∠B的度数.
解答: 解:过点D作DF⊥BC于点F
解:过点D作DF⊥BC于点F
∵AE⊥BC,DF⊥BC,AD=AE
∴四边形AEFD为正方形
∴AD=AE
∵AD=AE,BC=3AD
∴BE=AE
∴∠B=45°
故选B.
点评:此题主要考查学生对正方形的判定及等腰梯形的性质的综合运用能力.
分析:过点D作DF⊥BC于点F,已知AD=AF,AE⊥BC,DF⊥BC,从而可判定四边形AEFD为正方形,根据已知及正方形的性质可得到BE=AE,从而求得∠B的度数.
解答:
 解:过点D作DF⊥BC于点F
解:过点D作DF⊥BC于点F∵AE⊥BC,DF⊥BC,AD=AE
∴四边形AEFD为正方形
∴AD=AE
∵AD=AE,BC=3AD
∴BE=AE
∴∠B=45°
故选B.
点评:此题主要考查学生对正方形的判定及等腰梯形的性质的综合运用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.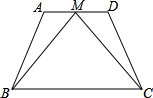 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.