题目内容
一个等边三角形的内切圆的半径为r、外接圆的半径为R，那么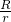
=________．
2
分析：首先根据题意画出图形，设圆心为O，内切圆与三角形相切于E、F、M点，连接OF、OA，由题意可知外接圆与内切圆属同心圆，故OA为外接圆的半径，OF为内切圆的半径，由∠OAF=30°，OF⊥AC，即可推出结论．
解答：
解：如图，连接OF、OA，
∵等边三角形ABC，
∴外接圆与内切圆属同心圆，
∴∠OAF=30°，OF⊥AC，
∴OA：OF=2：1，
∴R：r=2，
故答案为2．
点评：本题主要考查等边三角形的内切圆、外接圆的性质，等边三角形的性质，关键在于根据题意画出图形，作辅助线构建直角三角形，解直角三角形即可．
分析：首先根据题意画出图形，设圆心为O，内切圆与三角形相切于E、F、M点，连接OF、OA，由题意可知外接圆与内切圆属同心圆，故OA为外接圆的半径，OF为内切圆的半径，由∠OAF=30°，OF⊥AC，即可推出结论．
解答：
解：如图，连接OF、OA，∵等边三角形ABC，
∴外接圆与内切圆属同心圆，
∴∠OAF=30°，OF⊥AC，
∴OA：OF=2：1，
∴R：r=2，
故答案为2．
点评：本题主要考查等边三角形的内切圆、外接圆的性质，等边三角形的性质，关键在于根据题意画出图形，作辅助线构建直角三角形，解直角三角形即可．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
16、如图，等边三角形ABC中，AD⊥BC于D，△ABD的内切⊙O的半径为R，另有一个⊙O1与AB，BD，⊙O都相切，其半径为r1，则⊙O与⊙O1的面积之比为（ ）
