Question

如图，抛物线y=ax²+bx经过点A（4，0）、B（2，2），连接OB、AB．
（1）求抛物线的解析式；
（2）求证：△OAB是等腰直角三角形．

Answer 1

（1）解：由题意得 ，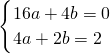
解得 ；
∴该抛物线的解析式为：y=-x²+2x；

（2）证明：过点B作BC⊥x轴于点C，则OC=BC=AC=2；
∴∠BOC=∠OBC=∠BAC=∠ABC=45°；
∴∠OBA=90°，OB=AB；
∴△OAB是等腰直角三角形；
分析：（1）将A、B的坐标代入抛物线的解析式中，通过联立方程组即可求出抛物线的解析式；
（2）过B作BC⊥x轴于C，根据A、B的坐标易求得OC=BC=AC=2，由此可证得∠BOC、∠BAC、∠OBC、∠ABC都是45°，即可证得△OAB是等腰直角三角形．
点评：此题主要考查了利用待定系数法求二次函数解析式、两点间的距离公式、勾股定理的逆定理．解题时，要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段OB、AB间的关系．