题目内容
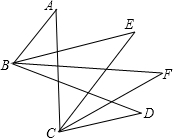 如图,∠ABD、∠ACD的平分线交于E,∠E=β1;∠EBD、∠ECD的平分线交于F,∠F=β2;如此下去,∠FBD、∠FCD的平分线的交角为β3;…若∠A=40°,∠D=32°,则β4为
如图,∠ABD、∠ACD的平分线交于E,∠E=β1;∠EBD、∠ECD的平分线交于F,∠F=β2;如此下去,∠FBD、∠FCD的平分线的交角为β3;…若∠A=40°,∠D=32°,则β4为分析:先根据角平分线的性质得出∠ABE=∠DBE,∠ACE=∠DCE,再由三角形外角的性质可得出∠BOC=∠E+∠ACE=∠A+∠ABE,∠BPC=∠E+∠DBE=∠D+∠DCE,再根据∠A=40°,∠D=32°即可得出∠E的度数,同理即可得出β2、β3、β4的度数.
解答:解:∵∠ABD、∠ACD的平分线交于E,∠EBD、∠ECD的平分线交于F,
∴∠ABE=∠DBE (1),
∠ACE=∠DCE (2),
∵∠BOC是△COE与△AOB的外角,
∴∠BOC=∠E+∠ACE=∠A+∠ABE (3),
∵∠BPC是△BEP与△PCD的外角,
∠BPC=∠E+∠DBE=∠D+∠DCE (4)
(3)+(4),得:2∠E+∠ACE+∠DBE=∠A+∠D+∠ABE+∠DCE (5)
把(1),(2),代入(5),
化简得:∠E=
=
=36°,
∴∠β1=36°,
同理可得,∠β2=
=
=
=34°,
∠β3=
=
=
=33°,
∴∠β4=
=
=32.5°.
故答案为:32.5.

∴∠ABE=∠DBE (1),
∠ACE=∠DCE (2),
∵∠BOC是△COE与△AOB的外角,
∴∠BOC=∠E+∠ACE=∠A+∠ABE (3),
∵∠BPC是△BEP与△PCD的外角,
∠BPC=∠E+∠DBE=∠D+∠DCE (4)
(3)+(4),得:2∠E+∠ACE+∠DBE=∠A+∠D+∠ABE+∠DCE (5)
把(1),(2),代入(5),
化简得:∠E=
| ∠A+∠D |
| 2 |
| 40°+32° |
| 2 |
∴∠β1=36°,
同理可得,∠β2=
| ∠E+∠D |
| 2 |
| ∠β1+∠D |
| 2 |
| 36°+32° |
| 2 |
∠β3=
| ∠F+∠D |
| 2 |
| ∠β2+∠D |
| 2 |
| 34°+32° |
| 2 |
∴∠β4=
| ∠β3+∠D |
| 2 |
| 33°+32° |
| 2 |
故答案为:32.5.

点评:本题考查的是三角形内角和定理及角平分线的性质、三角形外角的性质,根据以上知识求出β1、β2的度数,找出规律是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
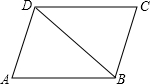 如图,△ABD≌△CDB,下面结论中不正确的是( )
如图,△ABD≌△CDB,下面结论中不正确的是( )| A、△ABD和△CDB的面积相等 | B、∠A+∠ABD=∠C+∠CBD | C、△ABD和△CDB的周长相等 | D、AD∥BC,且AD=BC |
 4、如图,∠ABD=90°,直线
4、如图,∠ABD=90°,直线 15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是
15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是 如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求
如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求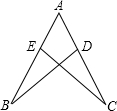 如图,△ABD≌△ACE,那么点B与点
如图,△ABD≌△ACE,那么点B与点