题目内容
阅读理解:对于任意正实数a、b,∵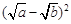 ≥0,∴
≥0,∴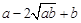 ≥0,
≥0,
∴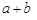 ≥
≥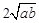 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在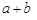 ≥
≥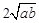 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥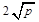 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值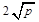 .
.
(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为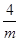 ,考虑何时时周长
,考虑何时时周长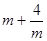 最小。
最小。
∵m>0,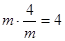 (定值),由以上结论可得:
(定值),由以上结论可得:
只有当m= 时,镜框周长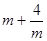 有最小值是 ;
有最小值是 ;
(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线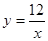 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.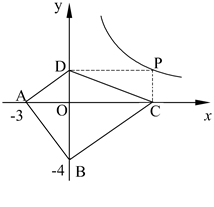
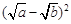 ≥0,∴
≥0,∴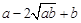 ≥0,
≥0,∴
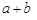 ≥
≥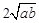 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.结论:在
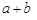 ≥
≥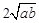 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥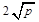 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值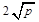 .
.(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为
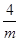 ,考虑何时时周长
,考虑何时时周长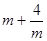 最小。
最小。∵m>0,
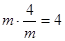 (定值),由以上结论可得:
(定值),由以上结论可得:只有当m= 时,镜框周长
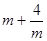 有最小值是 ;
有最小值是 ;(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线
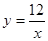 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(1)2,4
(2)设P(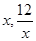 )
)
可得:
因为: (为定值)
(为定值)
所以: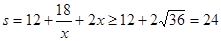
此时: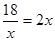 ,即:
,即: ,得:
,得: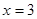
当: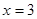 ,S最小为24,
,S最小为24,
此时,P(3,4),
OC=OA,OD=OB,∠COD=∠AOB
△OAB与△OCD全等。
(2)设P(
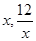 )
)可得:

因为:
 (为定值)
(为定值)所以:
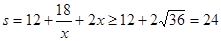
此时:
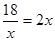 ,即:
,即: ,得:
,得: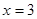
当:
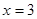 ,S最小为24,
,S最小为24,此时,P(3,4),
OC=OA,OD=OB,∠COD=∠AOB
△OAB与△OCD全等。
(1)根据式子特殊性可以分别求出m的值以及分式的最值;
(2)设P(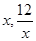 ),把四边形ABCD分割成四个小三角形,用含x的代数式表示出四边形ABCD的面积,根据式子特殊性可以分别求出代数式的最小值,并可得到点P的坐标,从而判断出△OAB与△OCD的关系.
),把四边形ABCD分割成四个小三角形,用含x的代数式表示出四边形ABCD的面积,根据式子特殊性可以分别求出代数式的最小值,并可得到点P的坐标,从而判断出△OAB与△OCD的关系.
(2)设P(
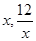 ),把四边形ABCD分割成四个小三角形,用含x的代数式表示出四边形ABCD的面积,根据式子特殊性可以分别求出代数式的最小值,并可得到点P的坐标,从而判断出△OAB与△OCD的关系.
),把四边形ABCD分割成四个小三角形,用含x的代数式表示出四边形ABCD的面积,根据式子特殊性可以分别求出代数式的最小值,并可得到点P的坐标,从而判断出△OAB与△OCD的关系.
练习册系列答案
相关题目
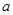 米,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天修路比原计划的2倍少40米,那么修这条路实际用了 天;
米,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天修路比原计划的2倍少40米,那么修这条路实际用了 天; 、
、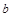 为实数,且
为实数,且 ,设
,设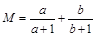 ,
,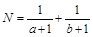 ,则
,则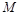 、
、 的大小关系 . (填 >, =, <)
的大小关系 . (填 >, =, <) 化为
化为 的形式,其中
的形式,其中 为常数,则
为常数,则 .
. 的结果为( )
的结果为( )

