题目内容
5．计算：（1）-9+12-（-3）
（2）-22÷4×[5-（-3）2]
（3）2a-5b-3a+b
（4）4（m2+n）+2（n-2m2）
分析 （1）原式利用减法法则变形，计算即可得到结果；
（2）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；
（3）原式合并同类项即可得到结果；
（4）原式去括号合并即可得到结果．
解答 解：（1）原式=-9+12+3=-9+15=6；
（2）原式=-4÷4×（-4）=4；
（3）原式=-a-4b；
（4）原式=4m2+4n+2n-4m2=6n．
点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
10．“十•一”黄金周期间，九寨沟风景区在7天假期中每天旅游的人数变化如表：（正数表示比9月30日多的人数，负数表示比9月30日少的人数）：
（1）若9月30日的游客人数记为a万人，请用含a的代数式表示10月2日的游客人数；
（2）请判断7天内游客人数最多和最少的各是哪一天，它们相差多少万人？
（2）若a=2，平均每人消费300元，请问风景区在这7天内总收入多少万元？
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 （万人） | +1.7 | +0.9 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
（2）请判断7天内游客人数最多和最少的各是哪一天，它们相差多少万人？
（2）若a=2，平均每人消费300元，请问风景区在这7天内总收入多少万元？
13．在数字1001000100010000中，0出现的频率是（ ）
| A． | 0.75 | B． | 0.8 | C． | 0.5 | D． | 12 |
20．下列说法中，正确的是（ ）
| A． | 0是最小的整数 | B． | 最大的负整数是-1 | ||
| C． | 任何有理数的绝对值都是正数 | D． | 一个有理数的平方总是正数 |
17．
如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（ ）
如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（ ）| A． | $y=\frac{9}{2x}$ | B． | $y=\frac{2}{9x}$ | C． | $y=\frac{{\sqrt{13}}}{x}$ | D． | $y=\frac{{\sqrt{13}}}{2x}$ |
14．某校八年级（1）班50名学生参加2007年济宁市数学质量监测考试，全班学生的成绩统计如下表：
请根据表中提供的信息解答下列问题：
（1）该班学生考试成绩的众数和中位数分别是多少？
（2）该班张华同学在这次考试中的成绩是83分，能不能说张华同学的成绩处于全班中偏上水平？试说明理由．
| 成绩（分） | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
（1）该班学生考试成绩的众数和中位数分别是多少？
（2）该班张华同学在这次考试中的成绩是83分，能不能说张华同学的成绩处于全班中偏上水平？试说明理由．
15．
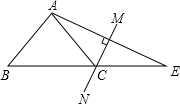如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C，且AB=CE，则∠B的度数是（ ）
如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C，且AB=CE，则∠B的度数是（ ）| A． | 45° | B． | 60° | C． | 50° | D． | 55° |