题目内容
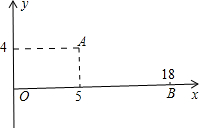 如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
分析:设截点为:C(x,0),然后根据速度的关系可得出x的一元二次方程,从而可得出最快截住的位置,然后利用待定系数法求解函数解析式即可.
解答:解:设截点为:C(x,0),则 BC=18-x,AC=
,
∴BC=2AC,
即可得:(18-x)2=4×[(5-x)2+16],
解得:x=8或-
,
∴最快在(8,0)出截住.
设机器人M行走路线对应的一次函数解析式为:y=kx+b,
,解得:
,
∴机器人M行走路线对应的一次函数解析式为:y=-
x+
.
| (5-x)2+42 |
∴BC=2AC,
即可得:(18-x)2=4×[(5-x)2+16],
解得:x=8或-
| 20 |
| 3 |
∴最快在(8,0)出截住.
设机器人M行走路线对应的一次函数解析式为:y=kx+b,
|
|
∴机器人M行走路线对应的一次函数解析式为:y=-
| 4 |
| 3 |
| 32 |
| 3 |
点评:本题考查了一次函数的综合,难度较大,解答本题的关键是根据题意设出截住的位置,利用方程的知识解出x的值,然后利用待定系数法求解函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 11、如图,一足球由黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,如果这种足球的白皮有20块,则黑皮有
11、如图,一足球由黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,如果这种足球的白皮有20块,则黑皮有
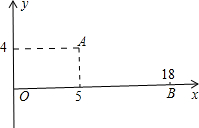 如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.