Question

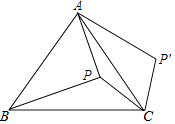
【题目】在三角形纸片ABC中，∠A=90°，∠C=30°，AC=30cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），减去△CDE后得到双层△BDE（如图2），再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为cm．

Answer 1

【答案】40或
【解析】解：∵∠A=90°，∠C=30°，AC=30cm， ∴AB=10 ，∠ABC=60°，
∵△ADB≌△EDB，
∴∠ABD=∠EBD= ABC=30°，BE=AB=10 ，
∴DE=10，BD=20，
如图1，平行四边形的边是DF，BF，且DF=BF= ，
∴平行四边形的周长= ，
如图2，平行四边形的边是DE，EG，且DF=BF=10，
∴平行四边形的周长=40，
综上所述：平行四边形的周长为40或 ，
所以答案是：40或 ．