Question

如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形，BE交AC于F，AD交CE于H.

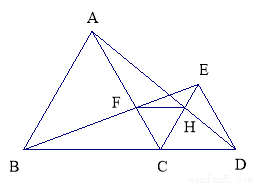
（1）证明：AB∥EC.

（2）求出∠ACE的度数.

（3）证明△ACD≌△BCE.

（4）判断△FCH为何种三角形并加以证明.

Answer 1

（1）证明见解析；（2）60°；（3）证明见解析；（4）△FCH是等边三角形.证明见解析.

【解析】

试题分析：（1）（2）由于△ABC和△CDE都是等边三角形，所以可知∠ACB=∠ECD=60°,从而可求出∠ACE=60°，又知∠BAC=60°，可证AB∥EC.

（3）由于△ABC和△CDE都是等边三角形，所以AC=BC,EC=DC，又∠FCE+∠BCF=∠DCE+∠ACE,从而可证△ACD≌△BCE.

由（3）知CF=CH,由（2）知∠ACE=60，从而得出△FCH是等边三角形.

试题解析：（1）、（2）∵△ABC和△CDE都是等边三角形

∴∠BAC=∠ACB=∠DCE=60°

∴∠ACE=180°-60°×2=60°;

AB∥EC.

（3）由△ABC和△CDE都是等边三角形知：

AC=BC, DC=EC ,∠ACB=∠ECD

∴∠ACB+∠ACE=∠ECD+∠ACE

∴∠ACD=∠BCE

∴△ACD≌△BCE.

（4）由（3）知：△ACD≌△BCE.

∴FC=HC

由（1）知：∠FCH=60°

△FCH是等边三角形.

考点：1全等三角形的判定与性质；2.等边三角形的判定与性质．