Question

【题目】如图，正方形ABCD的对角线AC与BD相交于O点，在BD上截取BE＝BC，连接CE，点P是CE上任意一点，PM⊥BD于M，PN⊥BC于N，若正方形ABCD的边长为1，则PM＋PN＝（ ）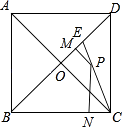

A.1
B.
C.
D.1＋

Answer 1

【答案】C
【解析】解：连接BP，作EH⊥BC，则PM．PN分别为△BPE和△BCP的高，且底边长均为1，

S△BCE＝1－ －S△CDE ，
∵DE＝BD－BE＝ ，△CDE中CD边上的高为 （ －1），
∵S△CDE＝CD× （ －1）＝ － ；
S△BCE＝1－ －S△CDE＝ ；
又∵S△BCE＝S△BPE＋S△BPC＝ BC（PM＋PN）
∴PM＋PN＝ ＝ ．
故答案为：C．
连接BP，作EH⊥BC，则PM．PN分别为△BPE和△BCP的高，且底边长均为1，根据题意可知：S△BCE＝S△BPE＋S△BPC，PM＋PN的长可求解。