题目内容
 如图,点A在反比例函数
如图,点A在反比例函数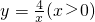 的图象上,点B在反比例函数
的图象上,点B在反比例函数 的图象上,且∠AOB=90°,则tan∠OAB的值为________.
的图象上,且∠AOB=90°,则tan∠OAB的值为________.

分析:首先过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,易得△OBD∽△AOC,又由点A在反比例函数
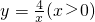 的图象上,点B在反比例函数
的图象上,点B在反比例函数 的图象上,即可得S△OBD=4.5,S△AOC=2,然后根据相似三角形面积的比等于相似比的平方,即可得
的图象上,即可得S△OBD=4.5,S△AOC=2,然后根据相似三角形面积的比等于相似比的平方,即可得 =
= ,然后由正切函数的定义求得答案.
,然后由正切函数的定义求得答案.解答:
 解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,∴∠ACO=∠ODB=90°,
∴∠OBD+∠BOD=90°,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∴∠OBD=∠AOC,
∴△OBD∽△AOC,
∴
 ,
,∵点A在反比例函数
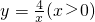 的图象上,点B在反比例函数
的图象上,点B在反比例函数 的图象上,
的图象上,∴S△OBD=4.5,S△AOC=2,
∴
 =
= ,
,∴tan∠OAB=
 =
= .
.故答案为:
 .
.点评:此题考查了相似三角形的判定与性质、反比例函数的性质以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.

练习册系列答案
相关题目
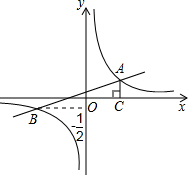 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0).
的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0). 上,求点D1的坐标;
上,求点D1的坐标;
 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数 (m≠0)的图象相交于A、B两点,且点B的纵坐标为
(m≠0)的图象相交于A、B两点,且点B的纵坐标为 ,过点A作AC⊥x轴于点C,AC=1,OC=2.
,过点A作AC⊥x轴于点C,AC=1,OC=2. (x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.
(x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.