题目内容
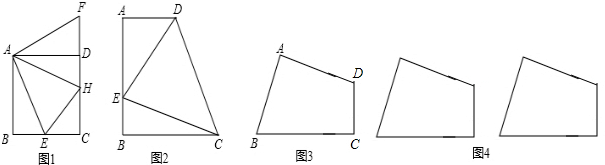
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE ,CF
,CF .
.

图1
(1)求 关于
关于 的函数解析式,并写出
的函数解析式,并写出 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证:  ;
;

图2
(3)在(2)的条件下,当 时,求
时,求 的值.
的值.
【答案】
(1)
 的取值范围是
的取值范围是
(2)略.
(3) ,
,
【解析】
试题分析:(1)由正方形ABCD可得, ,则
,则  ,
, 
即
(2)由(1)的结论得:
又

 ,即
,即 ,
, 
根据正方形ABCD的性质得 ,∴△OCF∽△EAC
,∴△OCF∽△EAC
故 .
.
(3) 在 △
△ 中,利用勾股定理得
中,利用勾股定理得
∵ ,
, 是公共角,
是公共角, , ∴根据相似三角形的性质三边对应成比例得
, ∴根据相似三角形的性质三边对应成比例得 ∴
∴
解得 ,
,
试题解析:(1)正方形ABCD中,DC∥AB,
∴ ,
即
,
即 .
(2分)
.
(2分)
∴
 的取值范围是
的取值范围是 ;
(2分)
;
(2分)
(2)∵ ,
,
∴ (2分)
(2分)
又∵
∴△OCF∽△EAC (2分)
∴ (1分)
(1分)
(3)在 △
△ 中,
中, (1分)
(1分)
∵ ,
, 是公共角,
是公共角,
∴△OCG∽ △ECA (2分)
∴ 
∴ , 解得
, 解得 ,
, (2分)
(2分)
经检验 ,
, 都是满足方程的解
都是满足方程的解
答(略)
考点:1.相似三角形的判定。2.相似三角形的性质。

练习册系列答案
相关题目

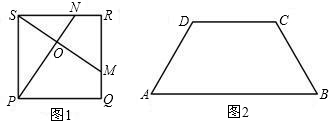 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明. 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.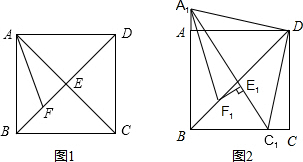 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.