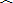题目内容
如图，弓形的面积为______．
连接OD，
∵AO是⊙O的半径，AO=4，CB是弓形的高，BC=2，
∴CO=4-2=2，
在Rt△OCA中，
根据勾股定理CA2=OA2-CO2，
即AC2=42-22=12，
∴AC=2
，
∴AD=4
，
∴sin∠AOC=
=
=
，
∴∠AOC=60°，∠AOD=120°，
∴S扇形OAD=
=
，
又S△AOD=
AD•OC=
×4
×2=4
，
∴S弓形ABD=S扇形OAD-S△AOD=
π-4
．
故答案为：
π-4
．
∵AO是⊙O的半径，AO=4，CB是弓形的高，BC=2，
∴CO=4-2=2，
在Rt△OCA中，
根据勾股定理CA2=OA2-CO2，
即AC2=42-22=12，
∴AC=2
| 3 |
∴AD=4
| 3 |
∴sin∠AOC=
| AC |
| AO |
2
| ||
| 4 |
| ||
| 2 |
∴∠AOC=60°，∠AOD=120°，
∴S扇形OAD=
| 120π×42 |
| 360 |
| 16π |
| 3 |
又S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S弓形ABD=S扇形OAD-S△AOD=
| 16 |
| 3 |
| 3 |
故答案为：
| 16 |
| 3 |
| 3 |
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
