题目内容
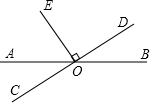如图，已知AB，CD相交于O，OE⊥CD于O，∠AOC=25°，则∠BOE的度数为________．
115°
分析：首先根据对顶角相等可得∠DOB=25°，再根据垂直定义可得∠EOD=90°，然后根据角的和差关系可得∠BOE的度数．
解答：∵∠AOC=25°，
∴∠DOB=25°，
∵OE⊥CD，
∴∠EOD=90°，
∴∠BOE=90°+25°=115°，
故答案为：115°．
点评：此题主要考查了垂线，关键是掌握当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．
分析：首先根据对顶角相等可得∠DOB=25°，再根据垂直定义可得∠EOD=90°，然后根据角的和差关系可得∠BOE的度数．
解答：∵∠AOC=25°，
∴∠DOB=25°，
∵OE⊥CD，
∴∠EOD=90°，
∴∠BOE=90°+25°=115°，
故答案为：115°．
点评：此题主要考查了垂线，关键是掌握当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．
练习册系列答案
轻松暑假总复习系列答案
相关题目
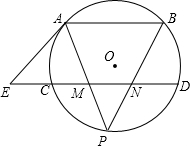如图，已知AB、CD是⊙O的两条平行弦，过A点的⊙O的切线AE和DC的延长线交于E点，P为弧
11、如图，已知AB=BC=CD=AD，∠DAC=40°，那么∠B=
如图，已知AB，CD相交于点0，△ACO≌△BD0，CE∥DF，求证：CE=DF．
如图，已知AB、CD相交于点O，OE⊥AB，∠EOC=28°，则∠AOD=