题目内容
如图，抛物线y=x2-2x-3与x轴交于A、B两点，与y轴交于点C.
（1）点A的坐标为?????????? 点B的坐标为????????? ，点C的坐标为???????? ；
（2）设抛物线y=x2-2x-3的顶点坐标为M，求四边形ABMC的面积.
【答案】
（1）（-1，0），（3，0），（0，-3）；（2）9.
【解析】
试题分析：（1）分别令x=0、y=0即可求出A、B、C的坐标；
（2）运用配方法求出顶点M的坐标，作出抛物线的对称轴，交x轴于点D，则四边形ABMC的面积=△AOC的面积+梯形OCMD的面积+△BDM的面积.
试题解析:(1) 由y=0得x2-2x-3=0．
解得x1=-1，x2=3．
∴点A的坐标（-1，0），点B的坐标（3，0）．
由x=0，得y=-3
∴点C的坐标（0，-3）
（2）如图：作出抛物线的对称轴，交x轴于点D，
由y=x2-2x-3=（x-1）2-4得
点M的坐标（1，-4）
四边形ABMC的面积=△AOC的面积+梯形OCMD的面积+△BDM的面积.
=
=9.
考点: 二次函数图象与性质.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
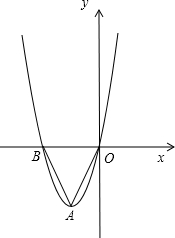如图，抛物线y=x2+4x与x轴分别相交于点B、O，它的顶点为A，连接AB，AO．
16、如图，抛物线y=-x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y
已知如图，抛物线y=x2+（k2+1）x+k+1的对称轴是直线x=-1，且顶点在x轴上方．设M是直线x=-1左侧抛物线上的一动点，过点M作x轴的垂线MG，垂足为G，过点M作直线x=-1的垂线MN，垂足为N，直线x=-1与x轴的交于H点，若M点的横坐标为x，矩形MNHG的周长为l．
（2013•扬州）如图，抛物线y=x2-2x-8交y轴于点A，交x轴正半轴于点B．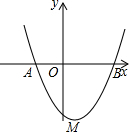
如图，抛物线y=x2-2x-3与x轴分别交于A，B两点．