题目内容
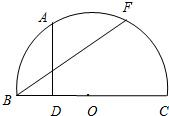 如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的中点,AD⊥BC于点D,求证:AD=
如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的中点,AD⊥BC于点D,求证:AD=| 1 | 2 |
分析:连接OA,根据垂径定理可知,BE=
BF,再证明△OAD≌△OBE,进而得到AD=BE,从而问题得证.
| 1 |
| 2 |
解答: 证明:连接OA,交BF于点E,
证明:连接OA,交BF于点E,
∵A是弧BF的中点,O为圆心,
∴OA⊥BF,
∴BE=
BF,
∵AD⊥BC于点D,
∴∠ADO=∠BEO=90°,
在△OAD与△OBE中,
,
∴△OAD≌△OBE(AAS),
∴AD=BE,
∴AD=
BF.
 证明:连接OA,交BF于点E,
证明:连接OA,交BF于点E,∵A是弧BF的中点,O为圆心,
∴OA⊥BF,
∴BE=
| 1 |
| 2 |
∵AD⊥BC于点D,
∴∠ADO=∠BEO=90°,
在△OAD与△OBE中,
|
∴△OAD≌△OBE(AAS),
∴AD=BE,
∴AD=
| 1 |
| 2 |
点评:本题主要考查了垂径定理及其推论,对于一个圆和一条直线,若直线具备①过圆心,②垂直于弦,③平分弦,④平分优弧,⑤平分劣弧这五条中任意两条,其他三条成立.

练习册系列答案
相关题目
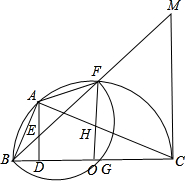 如图所示,已知BC是半圆O的直径,△ABC内接于⊙O,以A为圆心,AB为半径作弧交⊙O于F,交BC于G,交OF于H,AD⊥BC于D,AD、BF交于E,CM切⊙O于C,交BF的延长线于M,若FH=6,
如图所示,已知BC是半圆O的直径,△ABC内接于⊙O,以A为圆心,AB为半径作弧交⊙O于F,交BC于G,交OF于H,AD⊥BC于D,AD、BF交于E,CM切⊙O于C,交BF的延长线于M,若FH=6, 如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的中点,AD⊥BC于点D,求证:AD=
如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的中点,AD⊥BC于点D,求证:AD= BF.
BF.
 BF.
BF.