题目内容
如图,正三角形 的边长为
的边长为 .
.
(1)如图①,正方形 的顶点
的顶点 在边
在边 上,顶点
上,顶点 在边
在边 上.在正三角形
上.在正三角形 及其内部,以
及其内部,以 为位似中心,作正方形
为位似中心,作正方形 的位似正方形
的位似正方形 ,且使正方形
,且使正方形 的面积最大(不要求写作法);
的面积最大(不要求写作法);
(2)求(1)中作出的正方形 的边长;
的边长;
(3)如图②,在正三角形 中放入正方形
中放入正方形 和正方形
和正方形 ,使得
,使得 在边
在边 上,点
上,点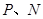 分别在边
分别在边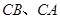 上,求这两个正方形面积和的最大值及最小值,并说明理由.
上,求这两个正方形面积和的最大值及最小值,并说明理由.
(无原图)
 的边长为
的边长为 .
.(1)如图①,正方形
 的顶点
的顶点 在边
在边 上,顶点
上,顶点 在边
在边 上.在正三角形
上.在正三角形 及其内部,以
及其内部,以 为位似中心,作正方形
为位似中心,作正方形 的位似正方形
的位似正方形 ,且使正方形
,且使正方形 的面积最大(不要求写作法);
的面积最大(不要求写作法);(2)求(1)中作出的正方形
 的边长;
的边长;(3)如图②,在正三角形
 中放入正方形
中放入正方形 和正方形
和正方形 ,使得
,使得 在边
在边 上,点
上,点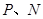 分别在边
分别在边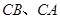 上,求这两个正方形面积和的最大值及最小值,并说明理由.
上,求这两个正方形面积和的最大值及最小值,并说明理由.(无原图)
(1)见解析(2) (3)
(3) ,
, ,理由见解析
,理由见解析
 (3)
(3) ,
, ,理由见解析
,理由见解析解:(1)如图①,正方形 即为所求.
即为所求.

(2)设正方形 的边长为
的边长为 .
.
∵△ 为正三角形,
为正三角形,
∴ .
.
∴ .
.
∴ ,即
,即 .(没有分母有理化也对,
.(没有分母有理化也对, 也正确)
也正确)
(3)如图②,连接 ,则
,则 .
.

设正方形 、正方形
、正方形 的边长分别为
的边长分别为
 ,
,
它们的面积和为 ,则
,则 ,
, .
.
∴ .
.
∴ .
.
延长 交
交 于点
于点 ,则
,则 .
.
在 中,
中, .
.
∵ ,即
,即 .
.
∴ⅰ)当 时,即
时,即 时,
时, 最小.
最小.
∴ .
.
ⅱ)当 最大时,
最大时, 最大.
最大.
即当 最大且
最大且 最小时,
最小时, 最大.
最大.
∵ ,由(2)知,
,由(2)知, .
.
∴ .
.
∴

 即为所求.
即为所求.
(2)设正方形
 的边长为
的边长为 .
.∵△
 为正三角形,
为正三角形,∴
 .
.∴
 .
.∴
 ,即
,即 .(没有分母有理化也对,
.(没有分母有理化也对, 也正确)
也正确)(3)如图②,连接
 ,则
,则 .
.
设正方形
 、正方形
、正方形 的边长分别为
的边长分别为
 ,
,它们的面积和为
 ,则
,则 ,
, .
.∴
 .
.∴
 .
.延长
 交
交 于点
于点 ,则
,则 .
.在
 中,
中, .
.∵
 ,即
,即 .
.∴ⅰ)当
 时,即
时,即 时,
时, 最小.
最小.∴
 .
.ⅱ)当
 最大时,
最大时, 最大.
最大.即当
 最大且
最大且 最小时,
最小时, 最大.
最大.∵
 ,由(2)知,
,由(2)知, .
.∴
 .
.∴



练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 中,对角线
中,对角线 、
、 交于点
交于点 ,
, 于
于 若
若
 则
则 .
.





