题目内容
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
(1)求证:AC∥DE;
(2)求证:过点B作BF⊥AC与点F,连接EF,试判断四边形BCEF的形状,并说明理由.

证明:(1)在矩形ABCD中,AB∥CD ∴∠CAB=∠DCA
∵∠EDC=∠CAB ∴∠EDC=∠DCA
∴AC∥DE ……………………………………………………………………………4分
(2)四边形BCEF为平行四边形
∵BF⊥AC ∴∠AFB=90°
∵∠E DC=∠CAB ∠DEC=∠AFB=90° CD=AB …………………………6分
DC=∠CAB ∠DEC=∠AFB=90° CD=AB …………………………6分
∴△DEC ≌△AFB
∴EC=FB ∠ECD=∠FBA ………………………………………………………6分
∵∠FBA+∠FBC=90° ∴∠ECD +∠DCB+∠FBC=180° ∴EC∥FB ………8分
∴四边形BCEF为平行四边形 ……………………………………………………10分

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 B.
B. C.
C.  D.
D. 
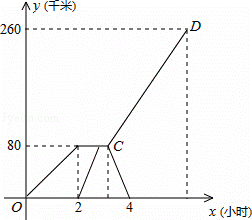
 ,其中
,其中 .
. 0名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是指 ( )
0名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是指 ( ) 学生的体重 D 被抽取的50名学生的体重
学生的体重 D 被抽取的50名学生的体重 C.(m5)5=m10 D.x2y3=(xy)5
C.(m5)5=m10 D.x2y3=(xy)5 位置上,则球拍击球的高度h应为( )
位置上,则球拍击球的高度h应为( )