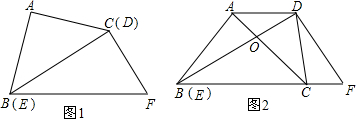Question

操作发现

将一副直角三角板如图（1）摆放,能够发现等腰直角三角板ABC的斜边BC与含30°角的直角三角板DEF的长直角边DE重合.

第20题图(1)

问题解决

将图（1）中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上.AC与BD交于点O,连接CD,如图（2）.

 (1)求证:△CDO是等腰三角形;

(2)若DF=8,求AD的长.

Answer 1

分析：(1)只要通过证明∠CDO=∠COD就可得到△CDO是等腰三角形.利用BC=BD，

∠DBC=30°,求出∠BDC=∠BCD=75°,而∠COD=45°+30°=75°，从而得出∠CDO

∠COD.

(2)过点D，A分别作出△BDF与△ABC的高，将梯形分成两个直角三角形和一个矩形后，利用解直角三角形和矩形的性质等知识求解.

(1)证明：由题图（1）知BC=DE,∴ ∠BDC=∠BCD.

∵ ∠DEF=30°,∴ ∠BDC=∠BCD=75°.

∵ ∠ACB=45°,∴ ∠DOC=30°+45°=75°.∴ ∠DOC=∠BDC.

∴ △CDO是等腰三角形.

(2)解：如图，过点A作AG⊥BC,垂足为点G,过点D作DH⊥BF,垂足为点H.

在Rt△DHF中,∠F=60°,DF=8,∴ DH=4,HF=4.

在Rt△BDF中,∠F=60°,DF=8,∴ BD=8,BF=16.

∴ BC=BD=8.

∵ AG⊥BC,∠ABC=45°,∴ BG=AG=4,∴ AG=DH.

∵ AG∥DH,∴ 四边形AGHD为矩形.∴ AD=GH=BF-BG-HF=16-4-4=12-4.