题目内容
 21、如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
21、如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.因为EF∥AD,
所以∠2=
∠3
(两直线平行,同位角相等
)又因为∠1=∠2
所以∠1=∠3(
等量代换
)所以AB∥
DG
(内错角相等,两直线平行
)所以∠BAC+
∠AGD
=180°(两直线平行,同旁内角互补
)因为∠BAC=80°
所以∠AGD=
100°
.分析:根据平行线的判定与性质填空.
解答:解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等);
又∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补),
∵∠BAC=80°,
∴∠AGD=100°.
∴∠2=∠3(两直线平行,同位角相等);
又∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补),
∵∠BAC=80°,
∴∠AGD=100°.
点评:本题考查平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 22、如图:EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.
22、如图:EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.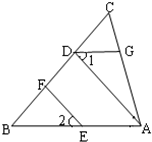 8、如图,EF∥AD,∠1=∠2,∠BAC=70°.则∠AGD=
8、如图,EF∥AD,∠1=∠2,∠BAC=70°.则∠AGD= 21、请把下列解题过程补充完整并在括号中注明理由:
21、请把下列解题过程补充完整并在括号中注明理由: 22、补全下面推理过程:
22、补全下面推理过程: 解:∵EF∥AD
解:∵EF∥AD 如图,EF∥AD,∠1=∠2,将求证AB∥DG的过程填空完整.
如图,EF∥AD,∠1=∠2,将求证AB∥DG的过程填空完整.