题目内容
△ABC的面积为1,顺次连接△ABC的各边中点组成△DEF(△DEF称为原三角形的第一个中点三角形),再顺次连接△DEF各边中点组成一个三角形,称为第二个中点三角形,…则按上述规律组成的第四个中点三角形的面积等于 .
【答案】分析:利用三角形相似比与面积的关系可知,第一个中点三角形的面积是总面积的 ,依此类推即可得出第四个三角形的面积是总面积的
,依此类推即可得出第四个三角形的面积是总面积的 .
.
解答:解:中点三角形与原三角形相似,相似比为 ,
,
故第一个中点三角形的面积是总面积的 ,
,
第二个中点三角形的面积是总面积的 ,
,
故第四个中点三角形的面积等于 =
= .
.
点评:考查利用相似比求解三角形的面积,并发现规律进行解题.
 ,依此类推即可得出第四个三角形的面积是总面积的
,依此类推即可得出第四个三角形的面积是总面积的 .
.解答:解:中点三角形与原三角形相似,相似比为
 ,
,故第一个中点三角形的面积是总面积的
 ,
,第二个中点三角形的面积是总面积的
 ,
,故第四个中点三角形的面积等于
 =
= .
.点评:考查利用相似比求解三角形的面积,并发现规律进行解题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
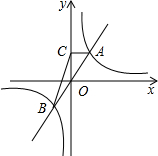 如图,正比例函数y=kx与反比例函数y=
如图,正比例函数y=kx与反比例函数y=| m |
| x |
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
 (2012•泰宁县质检)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(2012•泰宁县质检)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: 如图所示.△ABC中,AD⊥BC于D,E,F,G分别是AB、BD、AC的中点,若BC=
如图所示.△ABC中,AD⊥BC于D,E,F,G分别是AB、BD、AC的中点,若BC= 如图所示,已知AD是△ABC的边BC上的中线.
如图所示,已知AD是△ABC的边BC上的中线. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )
如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )