题目内容
【题目】(1)我们已经知道,在![]() 中,如果
中,如果![]() ,则
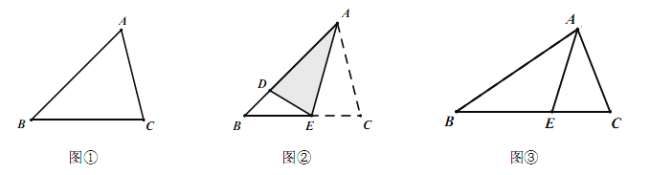
,则![]() ,下面我们继续研究:如图①,在
,下面我们继续研究:如图①,在![]() 中,如果
中,如果![]() ,则
,则![]() 与
与![]() 的大小关系如何?为此,我们把
的大小关系如何?为此,我们把![]() 沿
沿![]() 的平分线翻折,因为
的平分线翻折,因为![]() ,所以点
,所以点![]() 落在
落在![]() 边的点
边的点![]() 处,如图②所示,然后把纸展平,连接
处,如图②所示,然后把纸展平,连接![]() ,接下来,你能推出
,接下来,你能推出![]() 与
与![]() 的大小关系了吗?试写出说理过程.
的大小关系了吗?试写出说理过程.
(2)如图③,在![]() 中,
中,![]() 是角平分线,且
是角平分线,且![]() ,求证:
,求证:![]() .
.
(3)在(2)的条件下,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,则
,则![]() 的最小值为 .
的最小值为 .
【答案】(1)见解析 (2)见解析 (3)![]()
【解析】
(1)先根据图形折叠的性质得出∠ADE=∠C,再根据三角形外角的性质即可得出结论;
(2)在AB上截取AD=AC,连接DE.由于AE是角平分线,故可得出∠BAE=∠CAE,根据全等三角形的判定定理可得出△ADE≌△ACE,所以∠ADE=∠C,DE=CE,由三角形外角的性质可知,∠ADE=∠B+∠DEB,再由∠C=2∠B可得出∠B=∠DEB,所以AB=AD+DB,AD=AC,DB=DE=CE,由此即可得出结论.
(3) 如图,过C作CD![]() AB于D交AE于P,过P作PF
AB于D交AE于P,过P作PF![]() AC于F,这时
AC于F,这时![]() 取最小值,根据三角形ABC的面积公式可求得CD的长.
取最小值,根据三角形ABC的面积公式可求得CD的长.
(1)解:![]() ,理由如下:
,理由如下:
由折叠可知![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
(2)证明:如图,在![]() 上截取
上截取![]() ,连接
,连接![]()
∵![]() 平分
平分![]()
∴![]()
在![]() 和
和![]() 中
中

∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,img src="https://thumb.zyjl.cn/questionBank/Upload/2020/11/27/10/8a35f869/SYS202011271025518510232230_DA/SYS202011271025518510232230_DA.020.png" width="66" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
,img src="https://thumb.zyjl.cn/questionBank/Upload/2020/11/27/10/8a35f869/SYS202011271025518510232230_DA/SYS202011271025518510232230_DA.020.png" width="66" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
∵![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
∴![]()
∴![]()

(3)
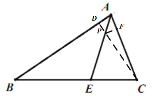
如图,过C作CD![]() AB于D交AE于P,过P作PF
AB于D交AE于P,过P作PF![]() AC于F,这时
AC于F,这时![]() 取最小值,
取最小值,
易知![]() ,
,
∴![]()
∵![]()
∴![]() 的最小值为
的最小值为![]() .
.









