Question

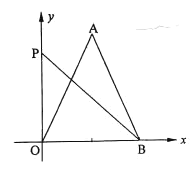
【题目】如图，已知平面直角坐标系中点坐标是，点在轴上， 是的垂直平分线上一点，是轴上一点，若时，则___________．

Answer 1

【答案】10

【解析】

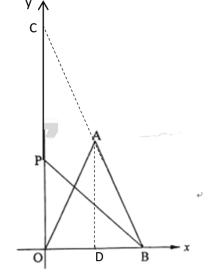
延长BA交y轴于点C，过点A作AD⊥OB于D，根据垂直平分线的性质、勾股定理、三线合一和点的坐标即可求出AO、AB、OB、AD的长，然后利用三角形外角的性质和等角对等边可得AC=AO，从而求出BC，根据勾股定理即可求出OC，再利用三角形外角的性质和等角对等边可得PB=PC，从而得出结论．

解：延长BA交y轴于点C，过点A作AD⊥OB于D

∵点坐标是，是的垂直平分线上一点

∴AO=AB ，OB=2OD=4， ∠OAB =2∠OAD，AD=5

根据勾股定理可得AB= AO=

∵PO⊥x轴

∴AD∥PO

∴∠OAD=∠AOP

∴∠OAB =2∠AOP

∵∠OAB=∠AOP＋∠ACO

∴∠AOP=∠ACO

∴AC=AO=

∴BC=AB＋AC=

根据勾股定理可得OC=

∵

∴∠OPB=2∠AOP=2∠ACO

∵∠OPB=∠ACO＋∠ABP

∴∠ACO=∠ABP

∴PB=PC

∴PO＋PC=OC=10

故答案为：10．