题目内容
 已知直线y=
已知直线y=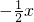 与抛物线y=
与抛物线y=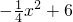 交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为
交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为
- A.12

- B.
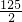
- C.
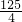
- D.
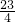
C
分析:根据直线y=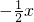 与抛物线y=
与抛物线y=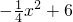 可以求出A、B两点的坐标,过点A作AM∥x轴,交抛物线于点M,作MC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F,则S△ABP=S四边形BCDP+S△PDA-S△ABC,就可以求出其值.
可以求出A、B两点的坐标,过点A作AM∥x轴,交抛物线于点M,作MC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F,则S△ABP=S四边形BCDP+S△PDA-S△ABC,就可以求出其值.
解答: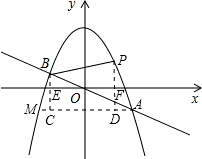 解:由题意,得
解:由题意,得
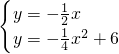
解得: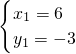 ,
,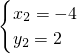 ,
,
∴A(6,-3),B(-4,2).
过点A作AM∥x轴,交抛物线于点M,作BC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F.
∴C(-4,-3),
∴BC=5,AC=10,
∴S△ABC=25,
设P(a,- a2+6),
a2+6),
∴PD=- a2+9,AD=6-a,
a2+9,AD=6-a,
∴S△PDA=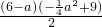 ,
,
S四边形BCDP=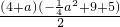
∴S△ABP=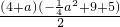 +
+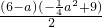 -25
-25
=-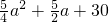
=-
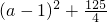 ,
,
∴当a=1时,S△ABP的最大值为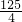 ,故C答案正确.
,故C答案正确.
故选C.
点评:本题是一道二次函数的综合试题,考查了利用函数的解析式求函数图象的交点坐标,图形的面积计算方法的运用,利用抛物线的解析式求最值.
分析:根据直线y=
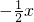 与抛物线y=
与抛物线y=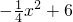 可以求出A、B两点的坐标,过点A作AM∥x轴,交抛物线于点M,作MC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F,则S△ABP=S四边形BCDP+S△PDA-S△ABC,就可以求出其值.
可以求出A、B两点的坐标,过点A作AM∥x轴,交抛物线于点M,作MC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F,则S△ABP=S四边形BCDP+S△PDA-S△ABC,就可以求出其值.解答:
 解:由题意,得
解:由题意,得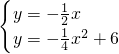
解得:
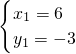 ,
,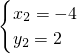 ,
,∴A(6,-3),B(-4,2).
过点A作AM∥x轴,交抛物线于点M,作BC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F.
∴C(-4,-3),
∴BC=5,AC=10,
∴S△ABC=25,
设P(a,-
 a2+6),
a2+6),∴PD=-
 a2+9,AD=6-a,
a2+9,AD=6-a,∴S△PDA=
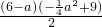 ,
,S四边形BCDP=
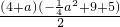
∴S△ABP=
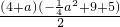 +
+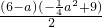 -25
-25=-
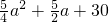
=-

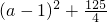 ,
,∴当a=1时,S△ABP的最大值为
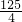 ,故C答案正确.
,故C答案正确.故选C.
点评:本题是一道二次函数的综合试题,考查了利用函数的解析式求函数图象的交点坐标,图形的面积计算方法的运用,利用抛物线的解析式求最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
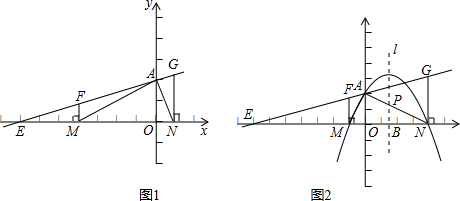
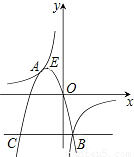
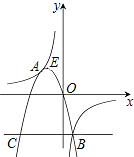 (2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线
(2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线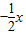 与抛物线y=
与抛物线y=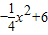 交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为( )
交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为( )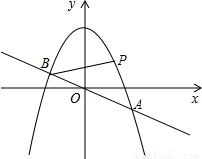
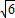
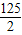
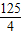
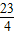
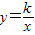 相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.