题目内容
【题目】如图，在直角坐标系中，点A（2，0），点B（0，1），过点A的直线l垂直于线段AB，点P是直线l上一动点，过点P作PC⊥x轴，垂足为C，把△ACP沿AP翻折180°，使点C落在点D处．若以A，D，P为顶点的三角形与△ABP相似，则所有满足此条件的点P的坐标为 ．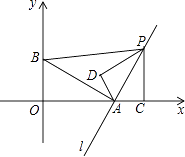 
【答案】P（4,4）,p（0,﹣4）,P（ 
,﹣1）,P（ 
,1）
【解析】解：∵点A（2，0），点B（0，1），
∴直线AB的解析式为y=﹣ 
x+1
∵直线l过点A（2，0），且l⊥AB，
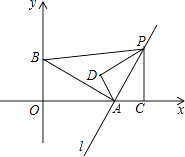
∴直线L的解析式为；y=2x﹣4，
∠BAO+∠PAC=90°，
∵PC⊥x轴，
∴∠PAC+∠APC=90°，
∴∠BAO=∠APC，
∵∠AOB=∠ACP，
∴△AOB∽△PCA，
∴ 
= 
，
∴ 
= 
= ，
设AC=m，则PC=2m，
∵△PCA≌△PDA，
∴AC=AD，PC=PD，
∴ 
= = ，
如图1：当△PAD∽△PBA时，
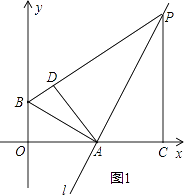
则 
= 
，
则 = 
= ，
∵AB= 
= 
，
∴AP=2 ，
∴m2+（2m）2=（2 ）2，
∴m=±2，
当m=2时，PC=4，OC=4，P点的坐标为（4，4），
当m=﹣2时，如图2，
PC=4，OC=0，P点的坐标为（0，﹣4），
如图3，若△PAD∽△BPA，
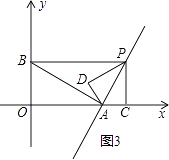
则 
= = ，
PA= AB= 
，
则m2+（2m）2=（ ）2，
∴m=± ，
当m= 时，PC=1，OC= ，P点的坐标为（ ，1），
当m=﹣ 时，如图4，PC=1，OC= ，P点的坐标为（ ，﹣1）；
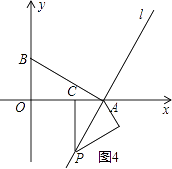
所以答案是：P（4，4），p（0，﹣4），P（ ，﹣1），P（ ，1）．
【考点精析】关于本题考查的勾股定理的概念和翻折变换（折叠问题），需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．
