题目内容
如图,在△ABC中,D是AB边的中点,PD⊥AB交∠ACB的平分线与点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N.
求证:CM=CN=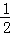 (AC+BC)
(AC+BC)
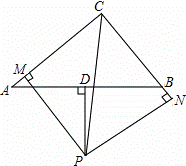
证明:连接AP,BP,
∵CP是∠ACB平分线,
∴PM=PN,
∵PD⊥AB,D是AB中点,
∴AP=BP,
在RT△APM和RT△BPN中,
 ,
,
∴RT△APM≌RT△BPN(HL),
∴AM=BN,
在RT△CPM和RT△CPN中,
 ,
,
∴RT△CPM≌RT△CPN(HL),
∴CM=CN,
∵CN=BC+BN,CM=AC﹣AM
∴CM=CN= (BC+BN+AC﹣AM)=
(BC+BN+AC﹣AM)= (BC+AC).
(BC+AC).


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
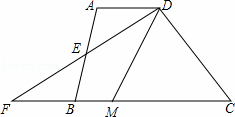
 .
.
 C.
C.  D.
D. 

 成绩的优秀率是多少?
成绩的优秀率是多少?