题目内容
(2007•徐州)如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.
【答案】分析:由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线;再利用角平分线的定义可知∠OBC+∠OCB= (∠ABC+∠ACB),代入数值即可求∠BOC=115°.
(∠ABC+∠ACB),代入数值即可求∠BOC=115°.
解答:解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (50°+80°)=65°,
(50°+80°)=65°,
∴∠BOC=180°-65°=115°.
点评:本题通过三角形内切圆,考查切线的性质.
 (∠ABC+∠ACB),代入数值即可求∠BOC=115°.
(∠ABC+∠ACB),代入数值即可求∠BOC=115°.解答:解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=
 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (50°+80°)=65°,
(50°+80°)=65°,∴∠BOC=180°-65°=115°.
点评:本题通过三角形内切圆,考查切线的性质.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
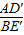 的值为1,求∠AFB的度数;
的值为1,求∠AFB的度数; ,BC=
,BC= ,①求
,①求 的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.

 的值为1,求∠AFB的度数;
的值为1,求∠AFB的度数; ,BC=
,BC=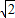 ,①求
,①求 的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
