Question

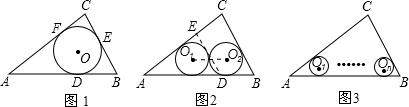
在Rt△ABC中，BC=3，AC=4，AB=5，
（1）如图1，D、E、F为切点，求△ABC内切圆⊙O的半径r₁的值．
（2）如图2△ABC中放置两个互相外切的等圆⊙O₁、⊙O₂，⊙O₁与AC、AB相切，⊙O₂与BC、AB相切，求它们的半径r₂时，小李同学是这样思考的：如果将⊙O₂连同BC边向左平移2r₂，使⊙O₂与⊙O₁重合、BC移到DE，则问题转化为第（1）问中的情况，于是可用同样的方法算出r₂，你认为小李同学的想法对吗？请你求出r₂的值（不限于上述小李同学的方法）．
（3）如图3，n个排成一排的等圆与AB边都相切，又依次外切，前后两圆分别与AC、BC边相切，求这些等圆的半径rn．

Answer 1

分析：（1）根据三角形的内切圆的半径的性质即可求解；
（2）（3）分别求出三角形的三边的长，根据三角形的内切圆的半径的性质即可求解．

解答：
解：（1）连OE、OF，则OE=OF=r₁
AD=AF，BD=BE，CE=CF，∠C=90°
∴四边形OECF是正方形，CE=CF=r₁
∴r₁=

1

2

（AC+BC-AB）=1

（2）平移后得到与△ABC相似的Rt△ADE三边长分别为
S-2r₁，

4

5

（5-2r₂），

3

5

（5-2r₂）．
则r₂=

1

2

【

4

5

（5-2r₂）+

3

5

（5-2r₁）-（5-2r₂）=

1

5

（5-2r₂）
∴r₂=

5

7

（3）将第n个圆连同BC边向左平移2（n-1）rn与第一个圆重合，所得直角三角形三边长为：
5-2（n-1）r_n，

4

5

【5-2（n-1）rn】，

3

5

【5-2（n-1）】
∴r_n=

1

5

【5-2（n-1）r_n】
∴r_n=

5

5+2(n-1)

=

5

3+2n

．

点评：本题主要考查了相切两圆的关系以及三角形的内切圆的性质，正确理解三角形的内切圆的半径的性质即可求解是解题的关键．