̀âÄ¿ÄÚÈƯ
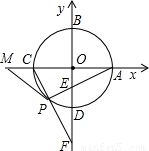
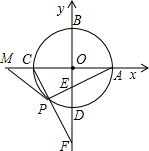 Èçͼ£¬̉Ô¡ÑOÁ½̀ơ»¥Ïà´¹Ö±µÄÖ±¾¶ËùÔÚÖ±ÏßΪÖὨÁ¢Æ½ĂæÖ±½Ç×ø±êϵ£¬Á½×ø±êÖá½»¡ÑOÓÚA£¬B£¬C£¬DËÄµă£¬µăPÔÚ»¡CDÉÏ£¬Á¬PA½»yÖáÓÚµăE£¬Á¬CP²¢ÑÓ³¤½»yÖáÓÚµăF£®
Èçͼ£¬̉Ô¡ÑOÁ½̀ơ»¥Ïà´¹Ö±µÄÖ±¾¶ËùÔÚÖ±ÏßΪÖὨÁ¢Æ½ĂæÖ±½Ç×ø±êϵ£¬Á½×ø±êÖá½»¡ÑOÓÚA£¬B£¬C£¬DËÄµă£¬µăPÔÚ»¡CDÉÏ£¬Á¬PA½»yÖáÓÚµăE£¬Á¬CP²¢ÑÓ³¤½»yÖáÓÚµăF£®£¨1£©Çó¡ÏFPEµÄ¶ÈÊư£»
£¨2£©ÇóÖ¤£ºOB2=OE•OF£»
£¨3£©Èô¡ÑOµÄ°ë¾¶Îª
| 3 |
| 5 |
| 2 |
| 3 |
£¨4£©ÔÚ£¨3£©µÄ̀ơ¼₫Ï£¬¹ưµăP×÷¡ÑOµÄÇĐÏßPMÓëxÖá½»ÓÚµăM£¬Çó¡÷PCMµÄĂæ»ư£®
·ÖÎö£º£¨1£©¸ù¾ƯÔ²ÖܽǶ¨Àí¿ÉÖª¡ÏAPC=90¡ă£¬ºÜÏÔÈ»¡ÏFPE=90¡ă£®
£¨2£©ºÜÏÔÈ»±¾̀ẩªÖ¤µÄÊÇ¡÷OCFºÍ¡÷OEAÏàËÆ£¬ƠâÁ½¸öÈư½ÇĐÎÖĐ̉ÑÖªµÄ̀ơ¼₫ÓĐ̉»×éÖ±½Ç£¬¶ø¡ÏOAEºÍ¡ÏOCFÊÇ̉»×é¶Ô¶¥½ÇµÄÓà½Ç̣̉´Ë̉²ÏàµÈ£¬µĂ³öƠâÁ½¸öÈư½ÇĐÎÏàËƺó¿ÉÖª£ºOA•OC=OE•OF£¬¶øOA=OB=OC£¬Óɴ˿ɵĂÖ¤£®
£¨3£©¸ù¾ƯΤ´ï¶¨Àí¿ÉÖªOE•OF=m£¬¸ù¾Ư£¨2£©µÄ½áÂÛ¿ÉÖª£ºOE•OF=3£¬̣̉´Ëm=3£¬¾Ư´Ë¿ÉÇó³öOE£¬OFµÄ³¤£¬¼´¿ÉµĂ³öFµÄ×ø±ê£®
¸ù¾ƯC¡¢FÁ½µăµÄ×ø±ê¿ÉÓĂ´ư¶¨ÏµÊư·¨Çó³öÖ±ÏßCFµÄ½âÎöʽ£®
£¨4£©¸ù¾Ư£¨2£©¿ÉµĂ³öEµăµÄ×ø±ê£¬̉²¾ÍÄÜÇó³öÖ±ÏßAEµÄ½âÎöʽ£¬ÁªÁ¢Ö±ÏßCFµÄ½âÎöʽ¼´¿ÉµĂ³öPµă×ø±ê£®
Á¬½ÓOP£¬ỘOP¡ÍPM£¬¿ÉÏÈÇó³öÖ±ÏßOPµÄ½âÎöʽ£¬È»ºó¸ù¾ƯOP¡ÍPMµĂ³öÖ±ÏßPMµÄ½âÎöʽ¼´¿ÉÇó³öMµăµÄ×ø±ê£®
̉ÑÖªÁËMµăµÄ×ø±ê¾ÍÄÜÇó³öMCµÄ³¤£¬È»ºó¸ù¾ƯPµă×Ư×ø±ê¼´¿ÉÇó³ö¡÷MCPµÄĂæ»ư£®
£¨Áí̉»Öֽⷨ£ºÏÈÔÚÖ±½ÇÈư½ÇĐÎAPCÖĐ£¬ÓĂACµÄ³¤ºÍ¡ÏCAPµÄÓàÏ̉ÖµÇó³öAPµÄ³¤£¬Í¬ÀíÇó³öPN£¬ANµÄ³¤£¬¼´¿ÉµĂ³öONµÄ³¤£®È»ºóÔÚÖ±½ÇÈư½ÇĐÎOPMÖиù¾ƯÉäÓ°¶¨ÀíÇó³öMNµÄ³¤£¬¼´¿ÉÇó³öMCµÄ³¤£¬̉ÑÖªÁËMCºÍPNµÄ³¤¼´¿ÉÇó³öÈư½ÇĐÎPMCµÄĂæ»ư£®£©
£¨2£©ºÜÏÔÈ»±¾̀ẩªÖ¤µÄÊÇ¡÷OCFºÍ¡÷OEAÏàËÆ£¬ƠâÁ½¸öÈư½ÇĐÎÖĐ̉ÑÖªµÄ̀ơ¼₫ÓĐ̉»×éÖ±½Ç£¬¶ø¡ÏOAEºÍ¡ÏOCFÊÇ̉»×é¶Ô¶¥½ÇµÄÓà½Ç̣̉´Ë̉²ÏàµÈ£¬µĂ³öƠâÁ½¸öÈư½ÇĐÎÏàËƺó¿ÉÖª£ºOA•OC=OE•OF£¬¶øOA=OB=OC£¬Óɴ˿ɵĂÖ¤£®
£¨3£©¸ù¾ƯΤ´ï¶¨Àí¿ÉÖªOE•OF=m£¬¸ù¾Ư£¨2£©µÄ½áÂÛ¿ÉÖª£ºOE•OF=3£¬̣̉´Ëm=3£¬¾Ư´Ë¿ÉÇó³öOE£¬OFµÄ³¤£¬¼´¿ÉµĂ³öFµÄ×ø±ê£®
¸ù¾ƯC¡¢FÁ½µăµÄ×ø±ê¿ÉÓĂ´ư¶¨ÏµÊư·¨Çó³öÖ±ÏßCFµÄ½âÎöʽ£®
£¨4£©¸ù¾Ư£¨2£©¿ÉµĂ³öEµăµÄ×ø±ê£¬̉²¾ÍÄÜÇó³öÖ±ÏßAEµÄ½âÎöʽ£¬ÁªÁ¢Ö±ÏßCFµÄ½âÎöʽ¼´¿ÉµĂ³öPµă×ø±ê£®
Á¬½ÓOP£¬ỘOP¡ÍPM£¬¿ÉÏÈÇó³öÖ±ÏßOPµÄ½âÎöʽ£¬È»ºó¸ù¾ƯOP¡ÍPMµĂ³öÖ±ÏßPMµÄ½âÎöʽ¼´¿ÉÇó³öMµăµÄ×ø±ê£®
̉ÑÖªÁËMµăµÄ×ø±ê¾ÍÄÜÇó³öMCµÄ³¤£¬È»ºó¸ù¾ƯPµă×Ư×ø±ê¼´¿ÉÇó³ö¡÷MCPµÄĂæ»ư£®
£¨Áí̉»Öֽⷨ£ºÏÈÔÚÖ±½ÇÈư½ÇĐÎAPCÖĐ£¬ÓĂACµÄ³¤ºÍ¡ÏCAPµÄÓàÏ̉ÖµÇó³öAPµÄ³¤£¬Í¬ÀíÇó³öPN£¬ANµÄ³¤£¬¼´¿ÉµĂ³öONµÄ³¤£®È»ºóÔÚÖ±½ÇÈư½ÇĐÎOPMÖиù¾ƯÉäÓ°¶¨ÀíÇó³öMNµÄ³¤£¬¼´¿ÉÇó³öMCµÄ³¤£¬̉ÑÖªÁËMCºÍPNµÄ³¤¼´¿ÉÇó³öÈư½ÇĐÎPMCµÄĂæ»ư£®£©
½â´đ£º½â£º£¨1£©¸ù¾ƯÔ²ÖܽǶ¨Àí£º¡ÏAPC=90¡ă£¬¡à¡ÏFPE=90¡ă£®
£¨2£©¡ß¡ÏOAE=¡ÏPFE=90¡ă-¡ÏOEA=90¡ă-¡ÏPEF£¬
¡à¡ÏOAE=¡ÏEFP£®
¡ß¡ÏAOE=¡ÏFOC=90¡ă£¬
¡à¡÷AOE¡×¡÷FOC£®
¡à
=
£®
¡ßOA=OB=OC£¬
¡àOB2=OE•OF£®
£¨3£©ÓÉ̀ẩâÖª£ºOE•OF=m=OB2=3£¬
¡àm=3£®
¡àx2-
x+3=0£¬½âµĂx=
£¬x=2
£®
¡ßOF£¾OE£¬
¡àOE=
£¬OF=2
£¬¼´E£¨0£¬-
£©£¬F£¨0£¬-2
£©£»
ÉèÖ±ÏßCFµÄ½âÎöʽΪy=kx+b£¬̉×Öª£ºC£¨-
£¬0£©£¬ỘÓĐ£º
£¬½âµĂ
£®
¡àÖ±ÏßCFµÄ½âÎöʽΪy=-2x-2
£®

£¨4£©¹ưP×÷PN¡ÍxÖáÓÚN£®
ÔÚÖ±½ÇÈư½ÇĐÎOAEÖĐ£¬OA=
£¬OE=
£¬̣̉´ËAE=
£®
ÔÚÖ±½ÇÈư½ÇĐÎACPÖĐ£¬AP=AC•cos¡ÏOAE=AC•
=2
•
=
£®
ÔÚÖ±½ÇÈư½ÇĐÎAPNÖĐ£¬PN=AP•sin¡ÏOAE=AP•
=
•
=
£»
AN=AP•cos¡ÏOAE=
•
=
£¬
¡àON=AN-OA=
£®
ÔÚÖ±½ÇÈư½ÇĐÎMPOÖĐ£¬¸ù¾ƯÉäÓ°¶¨Àí¿ÉµĂ£º
PN2=ON•MN£¬¡àMN=
£¬
¡àMC=MN+PN-OC=
£®
¡àS¡÷PCM=
•MC•PN=
¡Á
¡Á
=
£®
£¨2£©¡ß¡ÏOAE=¡ÏPFE=90¡ă-¡ÏOEA=90¡ă-¡ÏPEF£¬
¡à¡ÏOAE=¡ÏEFP£®
¡ß¡ÏAOE=¡ÏFOC=90¡ă£¬
¡à¡÷AOE¡×¡÷FOC£®
¡à
| OE |
| OC |
| OA |
| OF |
¡ßOA=OB=OC£¬
¡àOB2=OE•OF£®
£¨3£©ÓÉ̀ẩâÖª£ºOE•OF=m=OB2=3£¬
¡àm=3£®
¡àx2-
5
| ||
| 2 |
| ||
| 2 |
| 3 |
¡ßOF£¾OE£¬
¡àOE=
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
ÉèÖ±ÏßCFµÄ½âÎöʽΪy=kx+b£¬̉×Öª£ºC£¨-
| 3 |
|
|
¡àÖ±ÏßCFµÄ½âÎöʽΪy=-2x-2
| 3 |

£¨4£©¹ưP×÷PN¡ÍxÖáÓÚN£®
ÔÚÖ±½ÇÈư½ÇĐÎOAEÖĐ£¬OA=
| 3 |
| ||
| 2 |
| ||
| 2 |
ÔÚÖ±½ÇÈư½ÇĐÎACPÖĐ£¬AP=AC•cos¡ÏOAE=AC•
| OA |
| AE |
| 3 |
| ||||
|
4
| ||
| 5 |
ÔÚÖ±½ÇÈư½ÇĐÎAPNÖĐ£¬PN=AP•sin¡ÏOAE=AP•
| OE |
| AE |
4
| ||
| 5 |
| ||||
|
4
| ||
| 5 |
AN=AP•cos¡ÏOAE=
4
| ||
| 5 |
| ||||
|
8
| ||
| 5 |
¡àON=AN-OA=
3
| ||
| 5 |
ÔÚÖ±½ÇÈư½ÇĐÎMPOÖĐ£¬¸ù¾ƯÉäÓ°¶¨Àí¿ÉµĂ£º
PN2=ON•MN£¬¡àMN=
16
| ||
| 15 |
¡àMC=MN+PN-OC=
2
| ||
| 3 |
¡àS¡÷PCM=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
4
| ||
| 5 |
| 4 |
| 5 |
µăÆÀ£º±¾̀âΪ̉»´Îº¯Êư×ÛºÏ̀⣬Ö÷̉ª¿¼²éÁËÔ²µÄÏà¹Ø֪ʶºÍͼĐÎĂæ»ưµÄÇ󷨣¬ÄѶÈÊÊÖĐ£®

Á·Ï°²áϵÁĐ´đ°¸
 »¥¶¯Ó¢ÓïϵÁĐ´đ°¸
»¥¶¯Ó¢ÓïϵÁĐ´đ°¸
Ïà¹Ø̀âÄ¿
 £¨2013•ÉÜĐË£©Đ¡ĂôÔÚ×÷¡ÑOµÄÄÚ½ÓƠưÎå±ßĐÎʱ£¬ÏÈ×öÁËÈçϼ¸¸ö²½Ö裺
£¨2013•ÉÜĐË£©Đ¡ĂôÔÚ×÷¡ÑOµÄÄÚ½ÓƠưÎå±ßĐÎʱ£¬ÏÈ×öÁËÈçϼ¸¸ö²½Ö裺 Èçͼ£¬̉Ô¡ÑOÁ½̀ơ»¥Ïà´¹Ö±µÄÖ±¾¶ËùÔÚÖ±ÏßΪÖὨÁ¢Æ½ĂæÖ±½Ç×ø±êϵ£¬Á½×ø±êÖá½»¡ÑOÓÚA£¬B£¬C£¬DËÄµă£¬µăPÔÚ»¡CDÉÏ£¬Á¬PA½»yÖáÓÚµăE£¬Á¬CP²¢ÑÓ³¤½»yÖáÓÚµăF£®
Èçͼ£¬̉Ô¡ÑOÁ½̀ơ»¥Ïà´¹Ö±µÄÖ±¾¶ËùÔÚÖ±ÏßΪÖὨÁ¢Æ½ĂæÖ±½Ç×ø±êϵ£¬Á½×ø±êÖá½»¡ÑOÓÚA£¬B£¬C£¬DËÄµă£¬µăPÔÚ»¡CDÉÏ£¬Á¬PA½»yÖáÓÚµăE£¬Á¬CP²¢ÑÓ³¤½»yÖáÓÚµăF£® £¬̉ÔÏ߶ÎOE£¬OFµÄ³¤Îª¸ùµÄ̉»Ôª¶₫´Î·½³̀Ϊx2-
£¬̉ÔÏ߶ÎOE£¬OFµÄ³¤Îª¸ùµÄ̉»Ôª¶₫´Î·½³̀Ϊx2- x+m=0£¬ÇóÖ±ÏßCFµÄ½âÎöʽ£»
x+m=0£¬ÇóÖ±ÏßCFµÄ½âÎöʽ£»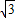 £¬̉ÔÏ߶ÎOE£¬OFµÄ³¤Îª¸ùµÄ̉»Ôª¶₫´Î·½³̀Ϊx2-
£¬̉ÔÏ߶ÎOE£¬OFµÄ³¤Îª¸ùµÄ̉»Ôª¶₫´Î·½³̀Ϊx2-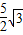 x+m=0£¬ÇóÖ±ÏßCFµÄ½âÎöʽ£»
x+m=0£¬ÇóÖ±ÏßCFµÄ½âÎöʽ£»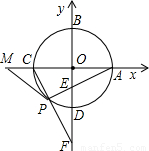
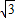 £¬̉ÔÏ߶ÎOE£¬OFµÄ³¤Îª¸ùµÄ̉»Ôª¶₫´Î·½³̀Ϊx2-
£¬̉ÔÏ߶ÎOE£¬OFµÄ³¤Îª¸ùµÄ̉»Ôª¶₫´Î·½³̀Ϊx2-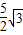 x+m=0£¬ÇóÖ±ÏßCFµÄ½âÎöʽ£»
x+m=0£¬ÇóÖ±ÏßCFµÄ½âÎöʽ£»